
傘は雨傘・日傘、和傘・洋傘の区別なく、通常、全体を支える中棒、全体を覆う傘布(カバー)、傘布を支える骨によって構成される。また、付属品として傘カバーや傘袋、バンドなどの周辺部品を付帯する。
UNICODEでは、雨傘は「U+2602」にコードポイントが割り振られている(☂)。
⇧ まさかの「UNICODE」に登録されてるとは、驚きを禁じ得ない今日この頃、どうもボクです。
というわけで、統計学についてです。
レッツトライ~。
t検定とは
Wikipediaさんに聞いてみよう。
t検定(ティーけんてい)とは、帰無仮説が正しいと仮定した場合に、統計量がt分布に従うことを利用する統計学的検定法の総称である。母集団が正規分布に従うと仮定するパラメトリック検定法であり、t分布が直接、もとの平均や標準偏差にはよらない(ただし自由度による)ことを利用している。
⇧ まぁ、分かり辛いんだけど、
⇧「仮説検定」の中の1手法という位置付けらしい。
ザックリとした関係は、
といった感じなんですかね?
「パラメトリック検定」には、「t検定」以外にもいろいろあるんだけど、「t検定」が利用されることが多いらしいです。
データサイエンスの研修を受講した時に講師の方に、『「検定統計量」を求める手法を決めるには何をもって判断すれば良いですか?』とお聞きしたところ、『「t検定」を使っておけば大丈夫』、との回答をいただいたので「t検定」に慣れておこうかと。
Scipyで「t検定」は主に3パターン
たぶん、Wikipediaの冒頭に『2組の標本について平均に有意差があるかどうかの検定などに用いられる。』 って説明があるからなのか、「scipy t検定」でググると、「2サンプルの場合」についての情報がトップに来てしまうというね...
そんな中で「1サンプル」の場合についても記載してくれてたのが、
⇧ 上記サイト様です。
上記サイト様を参考に、以下のパターンが存在する模様。
- 1サンプル
標本から得られた平均値が母集団の平均値と等しいのかを調べる - 2サンプル
2つのグループの平均値について差があるかを調べる- 対応のない t検定
2つの独立した母集団から標本を選んでくる場合 - 対応のある t検定
1つの母集団から標本を選んでくる場合
- 対応のない t検定
で、それぞれの「t検定」において、scipyの対応するメソッドの関係は、以下のようになるらしい。
| パターン | scipyのメソッド | |
|---|---|---|
| 1サンプル | stats.ttest_1samp | |
| 2サンプル | 対応のない t検定 | stats.ttest_ind |
| 対応のある t検定 | stats.ttest_rel | |
※ 上記で「scipyのメソッド」の名前だけ記載してますが、引数があるので、詳細はドキュメントなどで要チェック。
ちなみに、「3サンプル以上」になってくると、
この講義では、「分散分析」のうち、「一元配置分散分析」をとりあげます。 前回のt検定では2つの群の平均値を比較しましたが、分散分析は3つ以上の群の平均値を比較したり、ある条件の違いによって母平均が異なるかを検定します。
https://whitewell.sakura.ne.jp/PythonProbStat/Python-statistics6.html
⇧ ってな感じで「t検定」ではなく「分散分析」ってう手法を使って「検定統計量」を求めることになるみたいね。
実際に使ってみる
というわけで、実際に、「scipy」を使ってみますか。
ちなみに、今回は「Python」を使ってますが、「R」でも「t検定」はできます。
⇧ 上記のPDFのデータで試してみた。
「仮説検定」なので、
⇧ 「帰無仮説」と「対立仮説」を設定します。
今回の問題だと、
- 帰無仮説
μ(身長の平均)が、50.2 である - 対立仮説
μ(身長の平均)が、50.2 ではない
ってな仮説を立てるわけですと。
この時、気を付けたいのが、「帰無仮説」は、値が一つに定まるものにする必要がありますと。
⇧ 上記サイト様のコードを参考に実装。
「Google Cholaboratory」で以下のようにコーディングして、
import numpy as np
import scipy as sp
import scipy.stats as stats
from matplotlib import pyplot as plt
height = np.array([
51.0, 45.9, 48.8, 54.0, 53.5,
48.0, 44.5, 46.0, 50.3, 48.0
])
# 検定統計量
n = len(height) # サンプル数
k = n -1 # 自由度
u_var = np.var(height, ddof=1) # 不偏分散
statistical_sample_mean = np.mean(height) # 標本平均
# 仮説
statistical_population_mean = 50.2 # 母平均
t, p = stats.ttest_1samp(height, popmean=statistical_population_mean)
print("母平均が{0}のt値:{1}".format(statistical_population_mean, str(t)))
print("母平均が{0}である確率(p値):{1}".format(statistical_population_mean, str(p)))
# グラフ描画
x = np.linspace(-4, 4, 200)
flg, ax = plt.subplots(1, 1)
# t分布を描画
ax.plot(x, stats.t.pdf(x, k), linestyle="-", label="k="+str(k))
# t分布に今回の確率分布を表示させる
ax.plot(t, p, "x", color="red", markersize=7, markeredgewidth=2, alpha=0.8, label="experiment")
# t分布の95%信頼区間から外れた領域を描画する
bottom, up = stats.norm.interval(alpha=0.95, loc=0, scale=1)
plt.fill_between(x, stats.t.pdf(x, k), 0, where=(x>=up)|(x<=bottom), facecolor="black", alpha=0.1)
plt.xlim(-6, 6)
plt.ylim(0, 0.4)
plt.legend()
plt.show()
⇧ ってな感じで、実装。
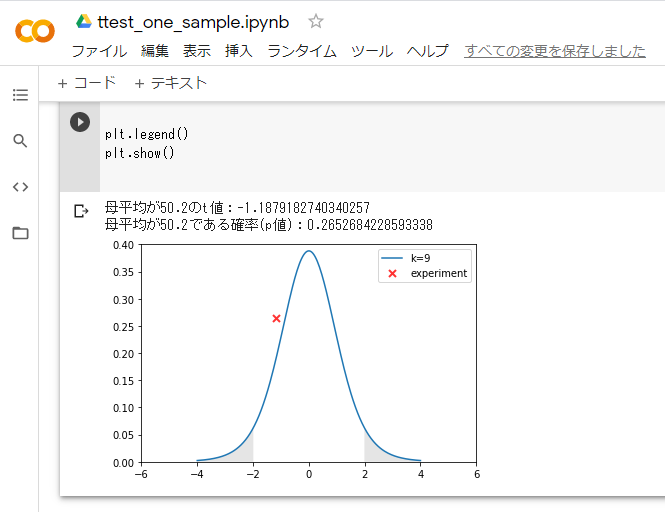
⇧ 上記のような結果になりました。
解答を見た感じ、
⇧ ピンク色の部分に「t値」が属していないので「帰無仮説」は「棄却」できないということのようです。
「母平均が50.2のt値:-1.1879182740340257」って結果だったので、上記の解答と同じく『「帰無仮説」は「棄却」できない』という結果になった模様。
続きまして、
⇧ 「2サンプル」の場合を試してみますか。
で、この場合、「等分散を仮定する」と言っているので、
ただし「対応なしt検定」を適用するためには、標本(=ここでは各クラスの成績データ)について、以下の条件を満たす必要があります。
- 2つの母集団から標本が無作為に抽出(ランダムサンプリング)されていること。
- 比較する2群のデータ(=各標本)の母集団が正規分布、またはそれに近い分布となっていること(正規性)。
- 比較する2群のデータ(=各標本)の分散が等しいこと(等分散性)。
⇧ 「対応なしt検定」を適応するってことになるらしいのですが、そのために「F検定」を実施する必要があるらしい、っていうか「t検定」以外を使う機会が早速訪れているんだが...
試してみる。
chemicalfactory.hatenablog.com
⇧ 上記サイト様で、2群をプロットする方法を参考にさせていただく。
import numpy as np
import scipy as sp
import scipy.stats as stats
from matplotlib import pyplot as plt
male_uric_acid_level = np.array([
5.1, 5.8, 5.2, 6.0, 6.3, 4.8, 6.8, 5.9, 5.9, 6.1, 5.6,
6.0, 5.3, 5.3, 3.6, 2.9, 6.3, 4.7, 5.7, 5.4, 7.1, 5.2
])
female_uric_acid_level = np.array([
5.0, 4.1, 4.2, 5.1, 3.5, 4.1, 4.8, 4.1, 4.8, 5.1, 5.1,
3.9, 4.7, 4.0, 3.9, 4.0, 5.0, 4.2, 5.1, 4.7, 3.9, 3.5
])
statistical_sample_mean_male = np.mean(male_uric_acid_level) # 標本平均
statistical_sample_mean_female = np.mean(female_uric_acid_level) # 標本平均
# F検定
male_var = np.var(male_uric_acid_level, ddof=1) # 不偏分散
female_var = np.var(female_uric_acid_level, ddof=1) # 不偏分散
male_degree_of_free = len(male_uric_acid_level) -1 # 自由度
female_degree_of_free = len(female_uric_acid_level) -1 # 自由度
f = male_var / female_var # F比の値
one_side_pval_1 = stats.f.cdf(f, male_degree_of_free, female_degree_of_free) # 片側検定のp値 1
one_side_pval_2 = stats.f.sf(f, male_degree_of_free, female_degree_of_free) # 片側検定のp値 2
two_side_pval = min(one_side_pval_1, one_side_pval_2) * 2 # 両側検定のp値
# 有意水準
significance_level = 0.01
# F検定のp値が、有意水準より大きければ、「等分散」といえるので、t検定を行う
if round(two_side_pval, 3) > significance_level:
t, p = stats.ttest_ind(male_uric_acid_level, female_uric_acid_level, equal_var=True)
print("t値:{0}, p値:{1}".format(t, p))
# グラフ用に自由度を配列に
degree_of_free_arr = [male_degree_of_free, female_degree_of_free]
# グラフ
x = np.linspace(-4, 4, 200)
flg, ax = plt.subplots(1, 1)
# t分布を描画
for i in range(0, len(degree_of_free_arr)):
ax.plot(x, stats.t.pdf(x, degree_of_free_arr[i]), linestyle="-", label="k="+str(degree_of_free_arr[i]))
# t分布に今回の確率分布を表示させる
ax.plot(t, p, "x", color="red", markersize=7, markeredgewidth=2, alpha=0.8, label="experiment")
# t分布の95%信頼区間から外れた領域を描画する
bottom, up = stats.norm.interval(alpha=0.95, loc=0, scale=1)
plt.fill_between(x, stats.t.pdf(x, degree_of_free_arr[i]), 0, where=(x>=up)|(x<=bottom), facecolor="black", alpha=0.1)
plt.xlim(-6, 6)
plt.ylim(0, 0.4)
plt.legend()
plt.show()
⇧ で実行してみた。

⇧ 考えてみたら、どっちも「サンプルのサイズ」が同じなので「自由度」が変わらないから、分布は重なって表示されますと...
解答はというと、
⇧ う、う~ん、「t値」が「4.74」ってことで、「t値:4.728720757245036」と微妙に異なるんだが、「0.01127924....」って許容範囲内と言えるのか...
まぁ、何て言うか、「検定統計量」を求める手法を決める方法が分からんのでモヤモヤ感が半端ないけども...
今回はこのへんで。





