https://en.wikipedia.org/wiki/Chi-square_distribution
In probability theory and statistics, the chi-square distribution (also chi-squared or χ2-distribution) with k degrees of freedom is the distribution of a sum of the squares of k independent standard normal random variables. The chi-square distribution is a special case of the gamma distribution and is one of the most widely used probability distributions in inferential statistics, notably in hypothesis testing and in construction of confidence intervals. This distribution is sometimes called the central chi-square distribution, a special case of the more general noncentral chi-square distribution.
⇧「自由度」が「k」の「カイ二乗分布」は「k個の独立した標準正規確率変数の2乗の合計の分布です」ということで、「カイ二乗分布」に従うらしい「カイ二乗検定」というものを試してみました。
ちなみに「自由度」はというと、
自由度(じゆうど、英語: degree of freedom)とは、一般に、変数のうち独立に選べるものの数、すなわち、全変数の数から、それら相互間に成り立つ関係式(束縛条件、拘束条件)の数を引いたものである。数学的に言えば、多様体の次元である。「自由度1」、「1自由度」などと表現する。
⇧ 分野で変わってくるみたいね。
「統計学」では、
統計学では、各種の統計量に関して自由度を定義している。
大きさ n の標本における観測データ (x1, x2, ..., xn) の自由度は n とする。それらから求めた標本平均 x についても同じ。
⇧ ってことみたいね。
それでは、レッツトライ~。
カイ二乗検定って?
Wikipediaさんに聞いてみる。
カイ二乗検定(カイにじょうけんてい、カイじじょうけんてい、英: Chi-squared test)、または検定とは、帰無仮説が正しければ検定統計量が漸近的にカイ二乗分布に従うような統計的検定法の総称である。
次のようなものを含む。
- ピアソンのカイ二乗検定:カイ二乗検定として最もよく利用されるものである(本項で述べる)。
- 一部の尤度比検定:標本サイズが大きい場合には近似的にカイ二乗検定となる場合がある。
- イェイツのカイ二乗検定(イェイツの修正)
- マンテル・ヘンツェルのカイ二乗検定
- 累積カイ二乗検定
- Linear-by-linear連関カイ二乗検定
⇧「仮説検定」で「検定統計量」を求める手法の中の一つってことですかね。
⇧「」とか変数名が紛らわしいな...
イェイツの補正(Yate's continuity correction)って?
Wikipediaさんに聞いてみた。
統計学において, イェイツの修正 (またはイェイツのカイ二乗検定)は分割表において独立性を検定する際にしばしば用いられる。場合によってはイェイツの修正は補正を行いすぎることがあり、現在は用途は限られたものになっている。
歴史を見てみると、
この推測はそこまで正確なものではなく、誤りを起こすこともある。 この推測の際の誤りによる影響を減らすため、英国の統計家であるフランク・イェイツは、2 × 2 分割表の各々の観測値とその期待値との間の差から0.5を差し引くことによりカイ二乗検定の式を調整する修正を行うことを提案した。
⇧ ってな感じで、「サンプル数」が少ないときを考慮して考案されたらしい。
だが、しかし!
この式は主に分割表の中の少なくとも一つの期待度数が5より小さい場合に用いられる。不幸なことに、イェイツの修正は修正しすぎる傾向があり、このことは全体として控えめな結果となり帰無仮説を棄却すべき時に棄却し損なってしまうことになりえる(第2種の過誤)。
そのため、イェイツの修正はデータ数が非常に少ない時でさえも必要ないのではないかとも提案されている。
⇧ 何と言うことでしょう!「第2種の過誤」が起こり得る可能性も上げることになってしまうんだとか...
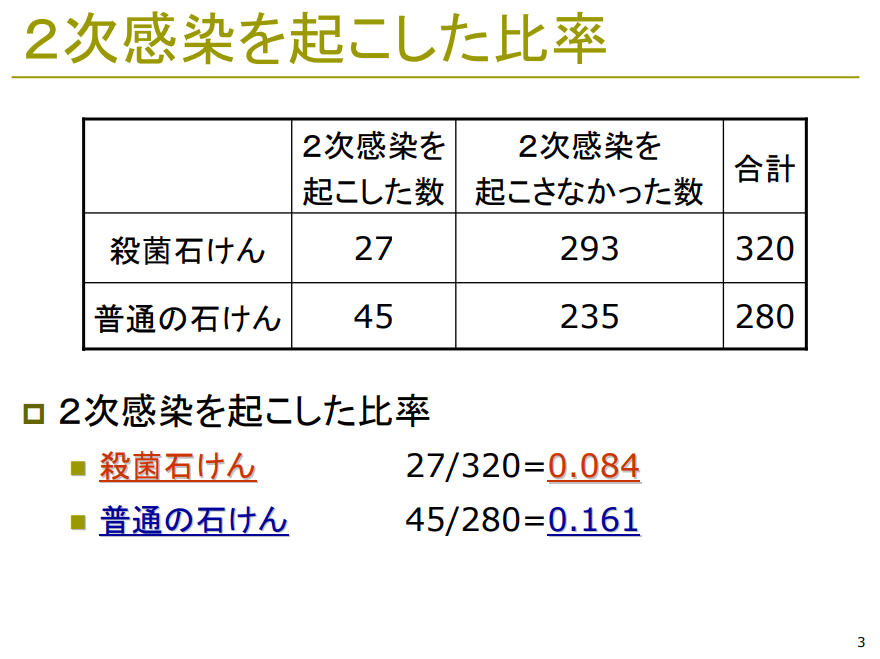
実際に「カイ二乗検定」してみる
というわけで、実際に「カイ二乗検定」してみますか。
⇧ 上記サイト様を参考に、実施していきます。
「帰無仮説」は以下となるようです。
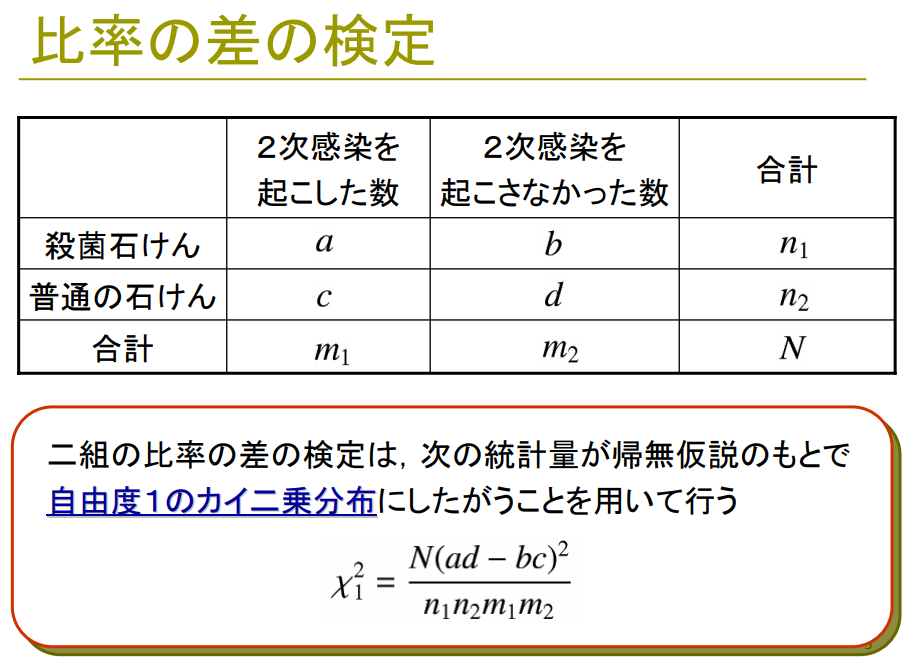
「二組の比率の差の検定」は「カイ二乗検定」を使っておけば良いんですかね?
というわけで、実際に試してみた。
⇧ 上記サイト様を参考にさせていただきました。
「Visual Studio Code」で実施しましたが、 「Google Colaboratry」とかでもコード自体は動くかと。(グラフの拡大とかが、「Google Colaboratry」だと無理っぽいかも)
「Visual Studio Code」を使う場合は、各種ライブラリを事前にインストールしておかないと、importできないので注意ですかね。
from scipy.stats import chi2
from scipy.stats import chi2_contingency
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
pd.set_option("display.unicode.east_asian_width", True)
# 元のデータが無いので、クロス集計がされた体で
result_crossed_df = pd.DataFrame([
[27, 293, 320],
[45, 235, 280],
[72, 528, 600]
],
index=["殺菌石けん", "普通の石けん", "合計"],
columns=["2次感染を起こした数", "2次感染を起こさなかった数", "合計"]
)
target_df = result_crossed_df.loc["殺菌石けん":"普通の石けん", ["2次感染を起こした数", "2次感染を起こさなかった数"]]
# 有意水準
significance_level = 0.01
print(target_df)
#手計算で「カイ二乗検定」
print("■手計算")
print(result_crossed_df["合計"].iat[2])
# x1 = 600*(27*235-293*45)**2/(320*280*72*528)
x2_manual_calculation = result_crossed_df["合計"].iat[2] * (result_crossed_df["2次感染を起こした数"].iat[0] * result_crossed_df["2次感染を起こさなかった数"].iat[1]-result_crossed_df["2次感染を起こさなかった数"].iat[0] * result_crossed_df["2次感染を起こした数"].iat[1])**2 / (result_crossed_df["合計"].iat[0] * result_crossed_df["合計"].iat[1] * result_crossed_df["2次感染を起こした数"].iat[2] * result_crossed_df["2次感染を起こさなかった数"].iat[2])
dof_manual_calculation = (len(target_df) -1) * (len(target_df.columns) -1)
print("カイ二乗値は %(x2_manual_calculation)s" %locals() )
print("自由度は %(dof_manual_calculation)s" %locals() )
# Scipyで「カイ二乗検定」
x2_yates_no, p_yates_no, dof_yates_no, expected_yates_no = chi2_contingency(target_df, correction=False)
x2_yates_yes, p_yates_yes, dof_yates_yes, expected_yates_yes = chi2_contingency(target_df)
print("■Scipy(イェイツの補正なし)")
print("カイ二乗値は %(x2_yates_no)s" %locals() )
print("確率は %(p_yates_no)s" %locals() )
print("自由度は %(dof_yates_no)s" %locals() )
print( expected_yates_no )
if p_yates_no < significance_level:
print("有意な差があります")
else:
print("有意な差がありません")
print("■Scipy(イェイツの補正あり)")
print("カイ二乗値は %(x2_yates_yes)s" %locals() )
print("確率は %(p_yates_yes)s" %locals() )
print("自由度は %(dof_yates_yes)s" %locals() )
print( expected_yates_yes )
if p_yates_yes < significance_level:
print("有意な差があります")
else:
print("有意な差がありません")
k = dof_yates_no
xc = chi2.ppf(1-significance_level, k)
print("Chi-square({0})={1}".format(significance_level, xc))
x_1 = np.linspace(0, xc*1.5, 100)
y_1 = chi2.pdf(x_1, k)
x_2 = np.linspace(xc, xc*1.5, 20)
y_2 = chi2.pdf(x_2, k)
y_max = round(np.max(y_1[y_1 != np.inf]), 1)
fig = plt.figure()
ax = fig.add_subplot(111)
ax.grid()
ax.plot(x_1, y_1, '-', color="blue", linewidth=1.0, label="k="+str(k))
ax.fill_between(x_2, y_2, '-', color="red")
ax.set_title("CHI-SQUARE DISTRIBUTION")
yticks = np.arange(0.0, y_max+0.1, 0.1)
yticklabels = ["%.2f" % x_1 for x_1 in yticks]
ax.set_yticks(yticks)
ax.set_yticklabels(yticklabels)
ax.legend()
ax.set_xlabel("x")
ax.set_ylabel("p(x)")
plt.show()
⇧ ってな感じで保存して、実行してみる。
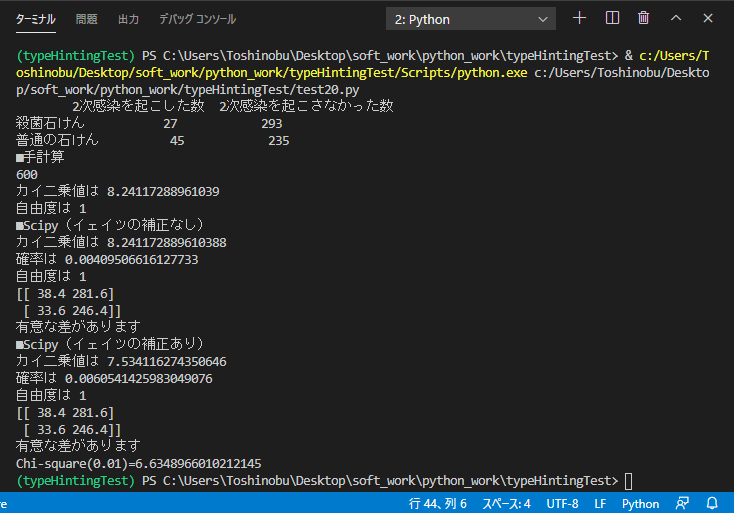
⇧「検定統計量(今回は、『カイ二乗値』のこと)」が、確かに「イェイツの補正」のありなしで変わってきますと。
グラフについては、
ルーペのアイコンを選択するとグラフの中で選択した部分を拡大できるので、 を選択します。
を選択します。
マウスでドラッグして、拡大したい範囲を選択で。
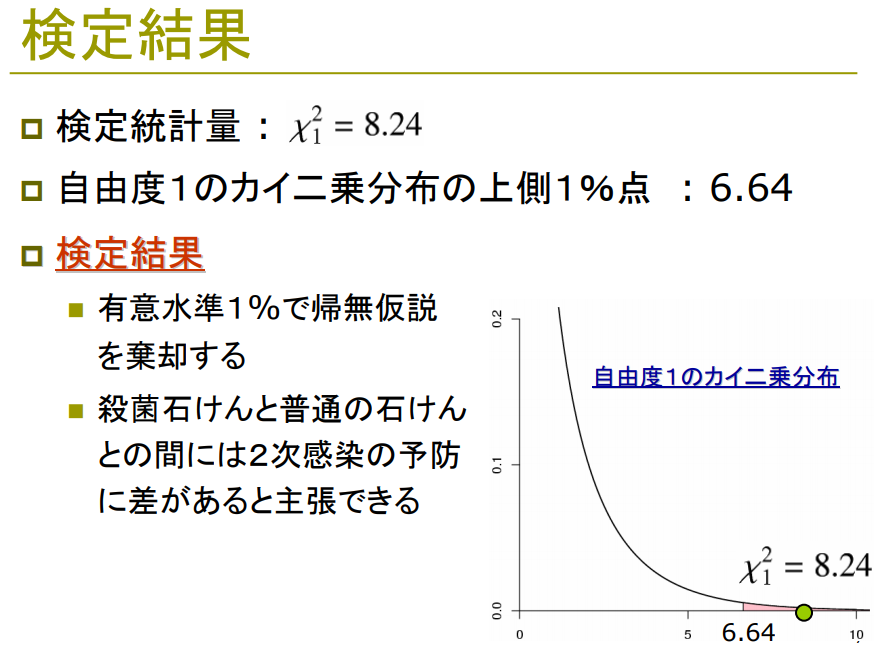
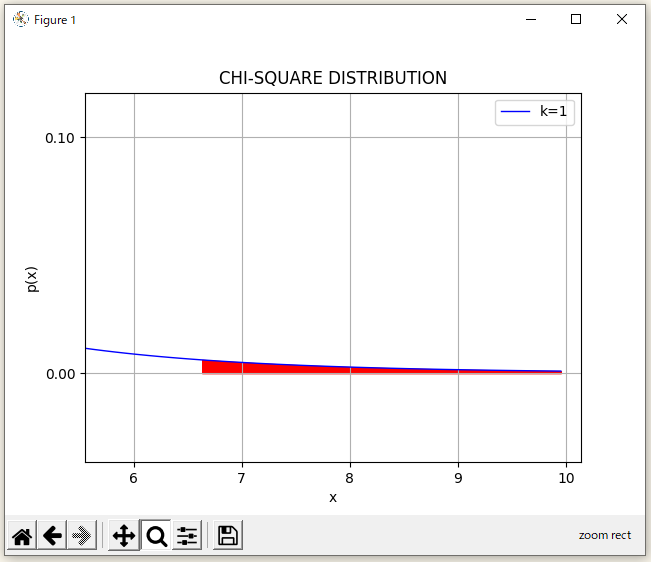
拡大された範囲を確認すると、赤い色で囲まれた面積の左端の が有意水準1%地点になるらしく検定統計量は
って値になるらしく(Scipyの結果は、
だけど)、今回の「カイ二乗検定」で算出した検定統計量が
(Scipyの結果は、
だけど)なので、「帰無仮説」を「棄却」できるってことみたい。
解答は、以下のような感じ。
⇧ ってな感じで、「イェイツの補正(Yate's continuity correction)」ありの場合の「検定統計量(今回は『カイ二乗値』)」も「7.534116274350646」だから、「有意水準」が「1%」の場合の「検定統計量(今回は『カイ二乗値』)」が「6.64」だから「帰無仮説」が「棄却」できるけども、「イェイツの補正(Yate's continuity correction)」には気を付ける必要がありますかね。
今回はこのへんで。