
⇧ 古代文字を解読できるAIとかできてたらしい。
⇧ 何てこった...YouTuberがピンポイントで狙われるなんて...Oh, my gosh
というわけで、
⇧ 行って参りました~。
数学の知識が無い人、どうもボクです。
今回は、セミナーの最後に、私のような数学の知識が無い人にも何とか伝わるように丁寧に解説してくれたりしてくれて、ありがたかったです。
そんでは、復習に、レッツトライ~。
機械学習は誤差を最小化したい
そもそも論なんですが、機械学習の目的って何ぞや?な情弱な私です。
機械学習の歴史なんかは、
・https://www.jstage.jst.go.jp/article/bjsiam/28/1/28_32/_pdf
⇧ 上記のPDFがまとまっています。
さて、どうして、難しい数式に満ちた関数を導出しないといけないん?って、そんな素朴な疑問を抱いていたのですが、セミナーで説明してくださりました。
ズバリ、『誤差の最小化』に尽きますと。
で、「誤差」って何のこと?
- 訓練誤差(経験損失)
- 汎化誤差
の2種類があるみたい。
機械学習をザックリ捉えると、「入力」が与えられたら、それに対する適切な「出力」を表現してくれる「関数」を見つけることですと。
ただ、実際には「入力」に対する「出力」は未知な訳ですと。(神のみぞ知るってやつですかね。)
なので、「訓練データ」というものを用意してあげて、仮の「出力」ってものを決めてしまいますと。
そうして、「訓練データ」を元に、「訓練データ」との「誤差」、つまり「訓練誤差(経験損失)」が「最小」となる「関数」を目指そうと。
ですが、「訓練データ」は推測に基づくデータであるため、データ自体に誤差が混入してる可能性があるため、正しくないデータであるという宿命を担っている「訓練データ」との「誤差」を「最小化」したところで、「真のデータ」との「誤差」が「最小化」されるとは限らないですと。(また、「無限」の「データ」を利用できるわけでなく、「有限個」の「データ」で対応する必要があるため、「不確実性」が常に存在するという懸念もありますと、全てを網羅できるわけではないから。)
「真のデータ」との「誤差」を「汎化誤差」というようです。
そして、「訓練誤差」と「汎化誤差」が乖離してしまうことを「過学習」というようです。
で、「訓練誤差」と「汎化誤差」の兼ね合いが激難らしく、
- 訓練データが少ないほど、訓練誤差は小さく、汎化誤差は大きくなる
- 訓練データが十分に多いと、訓練誤差も汎化誤差も、ノイズの強さで頭打ちになる
⇧ 「トレードオフ」的な関係になってそうですと。
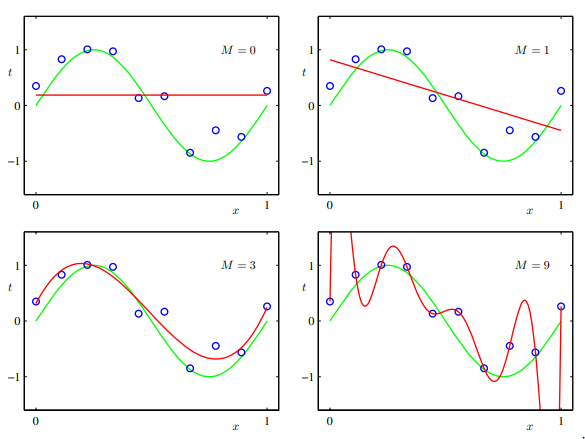
Bishop-Pattern-Recognition-and-Machine-Learning-2006.pdf
⇧ 「真の関数」が緑線で、「訓練データ」が青いマルで、「関数」は赤線で、「M」は「関数」の「次数」なんだけど、「9次関数(M=9)」になったときが「訓練データ」との「誤差」が最も最小となっているんだけど(青いマルを「関数」が全部通ってるので)、
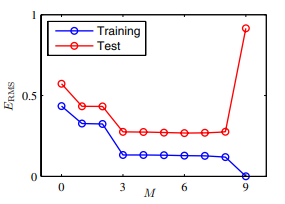
Bishop-Pattern-Recognition-and-Machine-Learning-2006.pdf
⇧ 赤が「汎化誤差」で、青が「訓練誤差」になるんだけど、「9次関数(M=9)」で最も乖離している、つまり「過学習」となってしまっていますと。「関数」の軌跡が「真の関数」の軌跡からかけ離れているためですね。
で、「訓練データ」が増えると、

Bishop-Pattern-Recognition-and-Machine-Learning-2006.pdf
⇧ 「真の関数」の軌跡と「関数」の軌跡の誤差が小さくなりますと。
上記のような試みを「最尤推定」って呼ぶようです。
⇧ 「最尤推定」は、「関数の次数」は「訓練データ」の量に依存してしまいますと。
ただ、「訓練データ」を増やし過ぎると、精度の担保ができませんということになるらしい、どれぐらいのデータ量を想定してるのかしら?(N=10000000000000000000000000000000000000000000000000000000000000000
とか?10の64乗、つまり「不可思議」)
ちなみに、
⇧ 上記サイト様によりますと、「10の68乗」の「無量大数」より大きい数字もあるそうな。
とりあえず、ここまでのようなアプローチで「関数」を求めていくのは「頻度主義」って方法になるようです。
頻度主義とベイズ主義と
「関数」を見つけるアプローチの仕方が、いろいろあって、今日までのセミナーだと(『パターン認識と機械学習 上』の内容では、第3章の途中)
| 手法 | アプローチ |
|---|---|
| 線形基底関数モデル | (最尤推定と最小二乗法、逐次学習、正則化最小二乗法) |
| ベイズ線形回帰 | (パラメータの分布、予測分布) |
って感じになりますと。
んで、世の中には「頻度主義」「ベイズ主義」なるものがありますと。
「統計学」的には、
⇧ 「尤度主義」ってのも入ってきますと。
今回は、「頻度主義」「ベイズ主義」の2つについてなのですが、
⇧ 上記スライドで違いを説明してくれています。
⇧ 上記スライドで違いを説明してくれています。
MCMCは、マルコフ連鎖モンテカルロ法(MCMC: Markov chain Monte Carlo methods)ってことらしい。
セミナーでも説明してくれていましたが、
| 方針 | 考え方 |
|---|---|
| 頻度主義 (frequentism) |
ただ1つの最適な値を捉えていこうとする試み |
| べイズ主義 (Bayesianism) |
1つに限定するのではなく、最適な値を含む分布として捉えていこうとする試み |
⇧ ザックリとしたイメージは上記のような感じになりますと。
確率の基本法則とベイズの定理
「機械学習」っていうのは「有限個」の「データ」で対応せざるを得ないため、「不確実性」が常に存在するわけですが、「不確実性」を考慮した考え方が存在しますと。
それが、「確率論」ですと。
確率論(かくりつろん、英: probability theory, 仏: théorie des probabilités, 独: Wahrscheinlichkeitstheorie)とは、偶然現象に対して数学的な模型(モデル)を与え、解析する数学の一分野である。
もともとサイコロ賭博といった賭博の研究として始まった。現在でも保険や投資などの分野で基礎論として使われる。
なお、確率の計算を問題とする分野を指して「確率論」と呼ぶ用例もあるが、本稿では取り扱わない。
現代数学の確率論は、アンドレイ・コルモゴロフの『確率論の基礎概念』(1933年)に始まる公理的確率論である。この確率論では「確率」が直接的に何を意味しているのかという問題は取り扱わず、「確率」が満たすべき最低限の性質をいくつか規定し、その性質から導くことのできる定理を突き詰めていく学問である。この確率論の基礎には集合論・測度論・ルベーグ積分があり、確率論を学ぶためにはこれらの知識が要求される。公理的確率論の必要性に関しては確率空間の項を参照。
現在、確率論は解析学の一分野として分類されている。特にルベーグ積分論や関数解析学とは密接なつながりがある。もちろん離散数学との関係も依然として深いが、離散的な場合であってもその内容は解析的なものであることが多い。また、確率論は統計学を記述する際の言語や道具としても重要である。
⇧ 「サイコロ賭博」の研究が起源という...ギャンブラーは偉大ですかな。
「確率論」では、「不確実性」が存在するものとして理論が構築されていますと。(「不確実性」が無かったら、みんなお金持ちになってしまいますからね。)
んで、確率の基本法則がありまして、
■加法定理
\begin{eqnarray} p(X) = \displaystyle \sum_{ Y } p(X, Y) \end{eqnarray}
■乗法定理
\begin{eqnarray} p(X, Y) = p(Y \mid X)p(X) \end{eqnarray}
ってな具合ですと。
⇧ 上記サイト様 によりますと、
- P(X) : X が起きる確率
- P(Y) : Y が起きる確率(事前確率と呼ぶ) )
- P(X | Y) : Y の後でXが起きる確率(条件付き確率・尤度と呼ぶ)
- P(Y | X) : X の後でY が起きる確率(条件付き確率・事後確率と呼ぶ)
って意味らしいです。
んで、「ベイズの定理」っていうのは、「乗法定理」から導けるらしいですと。
YとXの同時確率
\begin{eqnarray} p(X, Y) = p(Y \mid X)p(X) \end{eqnarray}
XとYの同時確率
\begin{eqnarray} p(Y, X) = p(X \mid Y)p(Y) \end{eqnarray}
は「対称性」により同じ値になりますと。(それぞれの確立は独立していて、互いに影響を与えることはないので。)
ということで、
\begin{eqnarray} p(X, Y) = p(Y, X) \end{eqnarray}
\begin{eqnarray} p(Y \mid X)p(X) = p(X \mid Y)p(Y) \end{eqnarray}
⇧ ってことが言えるので、
\begin{eqnarray} p(Y \mid X) = \frac{p(X \mid Y)p(Y)}{p(X)} \end{eqnarray}
⇧ っていう式が導かれ、これが「ベイズの定理」ってことみたい。
んで、「加法定理」 と「乗法定理」と「対称性」から、「ベイズの定理」の「分母」については、
\begin{align} p(X) &= \displaystyle \sum_{ Y } p(X, Y) \\ &= \displaystyle \sum_{ Y } p(Y, X) \\ &= \displaystyle \sum_{ Y } p(X \mid Y)p(Y) \end{align}
⇧ っていう形で現すことができるらしい。
「分母」が上記のように表現できるので、
\begin{eqnarray} p(Y \mid X) = \frac{p(X \mid Y)p(Y)}{\displaystyle \sum_{ Y } p(X \mid Y)p(Y)} \end{eqnarray}
⇧ っていう形で現せますと。
ちなみに、「ベイズの定理」の「分母」の部分は、「条件付き確率であるp(Y | X)をすべてのYについて和を取ったものが1になることを保証するための規格化(正規化)定数として見なすことができる」ってことらしいんだけど、よく分からん...
ベイズの定理の分母p(D)は周辺尤度、あるいはエビデンスと呼ばれます。
MAP推定は事後分布に対して最大化を行いますが、右辺を見たときの分母の値はに依存しておらず、ただの定数なので、通常は無視されます。事後分布が確率密度関数となること(つまり総和、あるいは積分が1)を保証するための正規化定数だと考えればいいでしょう。
⇧ え~っと、つまり、「ベイズの定理」の「分母」は、
\begin{eqnarray} p(X) = \displaystyle \sum_{ Y } p(X \mid Y)p(Y) \end{eqnarray}
⇧ 上記のように表現されていて、「Y」についての積分なので、
\begin{align} p(X) &= \displaystyle \sum_{ Y } p(X \mid Y)p(Y) \\ &= \int_y p(X \mid Y)p(Y) dy \end{align}
⇧ って形になるわけだから、p(X) については、定数であると言えるわけですと。
ちなみに、MAP推定は、
最大事後確率(さいだいじごかくりつ、英: maximum a posteriori, MAP)推定は、統計学において、実測データに基づいて未知の量の点推定を行う手法である。ロナルド・フィッシャーの最尤推定 (MLE) に密接に関連するが、推定したい量の事前分布を利用して最適化問題を解き確率が最大の結果を得る。したがってMAP推定は、最尤推定に正則化をつけた物と見ることもできる。
数学・統計学・計算機科学において、特に機械学習と逆問題において、正則化(せいそくか、英: regularization)とは、不良設定問題を解いたり過学習を防いだりするために、情報を追加する手法である。モデルの複雑さに罰則を科すために導入され、なめらかでないことに罰則をかけたり、パラメータのノルムの大きさに罰則をかけたりする。
正則化の理論的正当化はオッカムの剃刀にある。ベイジアンの観点では、多くの正則化の手法は、モデルのパラメータの事前情報にあたる。
⇧ 「正則化」ってのは「過学習」を防いだりするための情報追加らしい。
つまり、「ベイズ主義」でも「過学習」ってのは考慮すべきってことですかね?
さて、p(X) については、定数であるとの仮定に、「条件付き確率であるp(Y | X)をすべてのYについて和を取ったものが1になること」 って部分は矛盾しないか?
言葉通り、式にしてみると、p(X) については、定数であるから、
\begin{align}
\displaystyle \sum_{ Y } p(Y \mid X)
&= \displaystyle \sum_{ Y } \frac{p(X \mid Y)p(Y)}{\displaystyle \sum_{ Y } p(X \mid Y)p(Y)} = 1 \\
&= \frac{1}{\displaystyle \sum_{ Y } p(X \mid Y)p(Y)} \displaystyle \sum_{ Y } p(X \mid Y)p(Y) = 1 \\
&= \displaystyle \frac{1}{\int_y p(X \mid Y)p(Y) dy} \int_y p(X \mid Y)p(Y) dy = 1 \end{align}
⇧ みたいな形にできるはず。で、両辺に、定数であるp(X)をかけると、
\begin{align}
\displaystyle \sum_{ Y } p(Y \mid X)
&= \int_y p(X \mid Y)p(Y) dy = \int_y p(X \mid Y)p(Y) dy \end{align}
⇧ ってなるってことですかね?
「条件付き確率であるp(Y | X)をすべてのYについて和を取ったものが1になることを保証するための規格化(正規化)定数として見なすことができる」っていうか、「規格化(正規化)定数としないと、条件付き確率であるp(Y | X)をすべてのYについて和を取ったものが1にならない」 ってことだと思うんだけど...分からん。
「同時確立」 と「条件付き確率」の違いなんかは、
⇧ 上記サイト様が分かりやすいです。
⇧ 上記サイト様によりますと、表とか使うと良いらしい。
⇧ 集合が3つとかにも適応できますと。
ベイズ線形回帰
英語のWikipediaさんの力を借りましょう。
In statistics, Bayesian linear regression is an approach to linear regression in which the statistical analysis is undertaken within the context of Bayesian inference. When the regression model has errors that have a normal distribution, and if a particular form of prior distribution is assumed, explicit results are available for the posterior probability distributions of the model's parameters.
⇧ Google翻訳したところ、『「ベイズ推論」を使って「線形回帰」を行う。回帰モデルに正規分布を持つ誤差があり、「事前分布」の特定の形式が想定される場合、モデルのパラメーターの「事後確率分布」に対して明示的な結果が利用可能です。』ってことらしい。
ちなみに、「ベイズ推定」と「ベイズ推論」の違いはよく分かりませんでした。
日本語のWikipediaだと、
ベイズ推定(ベイズすいてい、英: Bayesian inference)とは、ベイズ確率の考え方に基づき、観測事象(観測された事実)から、推定したい事柄(それの起因である原因事象)を、確率的な意味で推論することを指す。
⇧ 「Bayesian inference」は「ベイズ推定」ってなってるけど...。
「ベイズ線形回帰」については、
⇧ 上記サイト様が分かりやすいです。
つまり、「線形回帰」を、「頻度主義」の手法で解くか、「ベイズ主義」の手法で解くかということらしく、「ベイズ主義」の手法で「線形回帰」を解くことを「ベイズ線形回帰」って言うそうな。
| 方針 | 内容 |
|---|---|
|
頻度主義 (frequentism) |
線形回帰 (linear regression)
|
|
ベイズ主義 (Bayesianism) |
ベイズ線形回帰 (Bayesian linear regression)
|
⇧ みたいな感じになるかと。
「共役事前分布」には、「正規分布」が選択されることが多いらしく、
確率論や統計学で用いられる正規分布(せいきぶんぷ、英: normal distribution)またはガウス分布(英: Gaussian distribution)は、平均値の付近に集積するようなデータの分布を表した連続的な変数に関する確率分布である。
何故、「正規分布」が「共役事前分布」に選ばれるのかは、
「データはもともとどれくらいずれてたの? 新しいデータがどれくらいずれるのかも見積もってね」
このような課題に対応すべく,
ランダムと言っても,
そんな
⇧ 上記サイト様が分かりやすいです。
なので、

Bishop-Pattern-Recognition-and-Machine-Learning-2006.pdf
⇧ 上図のような形の「正規分布」を「共役事前分布」として仮定するのが望ましいようです。
上記を踏まえて(「係数」を「w」、「入力」を「x」として、「w」と「x」 が定まった後で決まる「出力」を「t」とするので、上図とは微妙に変数が変わってます)、
■共役事前分布 条件付き分布
⇧ となるらしく、μ は、平均(mean)、σ の2乗っていうのは、分散(variance)で、分散の平方根である σ は、標準偏差(standard deviation)で、分散の逆数は β と表され、精度パラメータ(precision parameter)となるらしい。
平均(mean)である μ は、
分散の逆数 β は、
⇧ ってなるそうです。
で、「尤度関数」は、データ数を、Nとして考えた場合、 「入力」は、
「出力」は 、
の集合とみなせるので、「尤度関数」は、
■尤度関数
\begin{align}
p(\mathbf{T} \mid w, \mathbf{X}) &= p(t_i, ... t_n \mid w, x_i, ... x_n) \\
&= \displaystyle \prod_{ n = 1 }^N p(t_n \mid w, x_n) \end{align}
⇧ っていう「総乗」で表せるらしい。
ただ、総乗は計算がしにくい?のかは分かりませんが、両辺の対数をとって「対数尤度関数」として扱うのが良いようなので、
\begin{align}
\ln p(\mathbf{T} \mid w, \mathbf{X}) &= \displaystyle \sum_{ n = 1 }^N \ln p(t_n \mid w, x_n) \end{align}
⇧ というような形に変形できると。
対数については、
⇧ 上記サイト様を参考。
数式の記号なんかについては、
⇧ 上記サイト様を参考。
ここで、「共役事前分布 条件付き分布」では、以下のようになっていたので、
⇧ 上記の「対数尤度関数」を考えてみると、μ については、次数が2であるから、
⇧ 上記は、f(x)についての二次関数とみなさせて、且つ、w は定数とみなせますと。
なので定数項を「C」とすると、「対数尤度関数」は、
\begin{align}
\ln p(\mathbf{T} \mid w, \mathbf{X}) &= \frac{1}{2} \beta \displaystyle \sum_{ n = 1 }^N \left(t_n -\displaystyle \sum_{ i = 1 }^M w_i{\phi_i}(x_n)\right)^2 + C \end{align}
⇧ と表せるらしい。
で、「対数尤度関数」の形は、「線形回帰」の時に利用した「最小2乗法」の式にかなり似ているらしいです。
◇最小2乗法
\begin{align} E(w) &= \frac{1}{2} \displaystyle \sum_{ n = 1 }^N (f(x_n) - tn)^2 \\ &= \frac{1}{2} \displaystyle \sum_{ n = 1 }^N \left(\displaystyle \sum_{ i = 1 }^M w_i{\phi_i}(x_n) - t_n \right)^2 \end{align}
⇧ 確かに、かなり似た形ですな。
んで、w は以下の式で求まるらしい...何でこんな式になるのか全く謎だけど...
\begin{eqnarray} w = (\phi^T \phi)^{-1}\phi^T t \end{eqnarray}
ただし、
\begin{eqnarray} \phi = \left( \begin{array}{ccc}
\phi_{1}(x_1) & \phi_{2}(x_1) & \ldots & \phi_{M}(x_1) \\
\vdots & \vdots & \qquad & \vdots \\
\phi_{1}(x_N) & \phi_{2}(x_N) & \ldots & \phi_{M}(x_N)
\end{array} \right) \end{eqnarray}
⇧ 上記までは、確率化した「線形回帰」ってことらしく、まだベイズの要素が入ってなかったらしい。
⇩ ここから、ベイズの要素が入ってくる感じになるかと。
求めるべき「事後分布」と「事前共役分布」の関係は、
\begin{eqnarray} 事後分布 \ \propto \ 尤度関数 \times 共役事前分布 \end{eqnarray}
⇧ ってな感じになりますと。
ここで、「条件付き分布」は、
\begin{eqnarray} p(t \mid w, x) \end{eqnarray}
⇧ 上記のように表せていましたと。
実際には複数のデータ点を扱うので,
⇧ ってことで、「条件付き分布」は、
\begin{eqnarray} p(t \mid w) \end{eqnarray}
⇧ 上記のように表せることになりますと。
まずは事前分布,
そのp(w)とデータ点(x,t)を使って,
事後分布への更新式はベイズ公式と乗法・
⇧ ってことらしく、「事後分布」は、「ベイズの定理」から、
\begin{eqnarray} p(w \mid t) = \frac{p(t \mid w) p(w)}{p(t)} \end{eqnarray}
\begin{align} p(t) &= \int p(t, w) dw \\ &= \int p(t \mid w) p(w) dw \end{align}
⇧ 上記のようになりますと。
■共役事前分布
⇧ ということで、
\begin{eqnarray} p(w) = \mathcal{N}(w \mid 0, \alpha^{-1} \mathbf{\mathit{I}}) \end{eqnarray}
⇧ 上記のような「共役事前分布」を導入する感じで良いらしい。
■関数(事後分布)
「共役事前分布」を当てはめると、
\begin{align} p(w \mid t) &= \frac{p(t \mid w) p(w)}{p(t)} \\ &= \frac{ 1 }{ p(t)(2 \pi \alpha^{-1})^{\frac{M}{2}}(2 \pi \beta^{-1})^{\frac{1}{2}} }\exp \left\{-\frac{\beta}{2}(t - w^T{\phi}(x))^2 - \frac{\alpha}{2}w^Tw \right\} \end{align}
⇧ というような形になるようです。
さらに、2次形式というものに変形し、exp の前の部分を、1/Z' とすると、
\begin{eqnarray} p(w \mid t) = \frac{1}{Z’} \exp \left\{-\frac{1}{2}(w - m)^T \scriptsize{\sum}\nolimits_{ }^{ -1 } \normalsize{ (w - m)} \right\} \end{eqnarray}
ただし、
\begin{eqnarray} m = \beta \scriptsize{\sum} \normalsize{\phi (x)} \end{eqnarray}
\begin{eqnarray} \scriptsize{\sum}\nolimits_{ }^{ -1 } = \normalsize{\alpha \mathbf{\mathit{I}} + \beta \phi (x) \phi (x)^T} \end{eqnarray}
となるようです。
このときの、
\begin{eqnarray} \scriptsize{\sum} \end{eqnarray}
は、「総和」のシグマのことではなくて、「共分散行列」というものらしいです。
⇧ 上記サイト様によりますと、2次元の正規分布における「共分散行列」は、
\begin{eqnarray} \scriptsize{\sum} = \normalsize{\begin{bmatrix} S_x^2 & S_{xy} \\ S_{xy} & S_y^2 \end{bmatrix}} \end{eqnarray}
みたいな形 になり、「共分散行列」の逆行列は、
\begin{eqnarray} \scriptsize{\sum}\nolimits_{ }^{ -1 } = \normalsize{\frac{1}{\sum}} = \normalsize{\begin{bmatrix} S_y^2 & -S_{xy} \\ -S_{xy} & S_x^2 \end{bmatrix} } \end{eqnarray}
となるみたい。
Z' は、exp の部分の正規化係数とみなせるので、定数であると考えることができるため計算不要らしいです。
事後分布は、
\begin{eqnarray} p(w \mid t) = \mathcal{N}(w \mid m, \scriptsize{\sum} \normalsize{)} \end{eqnarray}
となり、正規分布でもあるので、
しかも,
⇧ とあるので、N個のデータの「共役事前分布」として利用できるらしく、
\begin{eqnarray} x=(x_1,……,x_N)^T \end{eqnarray}
\begin{eqnarray} t=(t_1,……,t_N)^T \end{eqnarray}
⇧ のようなデータの集合があれば、
\begin{eqnarray} p(w \mid t, x) = \mathcal{N}(w \mid m_N, \scriptsize{\sum}\nolimits_N \normalsize{)} \end{eqnarray}
ただし、
\begin{eqnarray} m_N = \beta \scriptsize{\sum}\nolimits_N \normalsize{\phi^T t} \end{eqnarray}
\begin{eqnarray} \scriptsize{\sum}\nolimits_N^{-1} = \normalsize{\alpha \mathbf{\mathit{I}} + \beta \phi^T \phi}
\end{eqnarray}
⇧ となるみたい。
⇧ のように
wの事後分布p(w|t)=N(w|μN,ΣN)は正規分布ですから,
⇧ とあり、w も求まりますと。
このように事後分布の最大点をwの推定値とみなす手法には,
⇧ MAP推定が出て参りました。
\begin{eqnarray} さらに、 m_N は、\end{eqnarray}
\begin{align} m_N &= \beta \scriptsize{\sum}\nolimits_N \normalsize{\phi^T t} \\ &= \beta (\alpha \mathbf{\mathit{I}} + \beta \phi^T \phi )^{-1} \phi^T{t} \\
&= \left(\left(\frac{\alpha}{\beta}\right) \mathbf{\mathit{I}} + \phi^T \phi \right)^{-1} \phi^T{t} \end{align}
⇧ と表せて、この形は、正則化付きの「線形回帰」である以下の形状とほぼ一致しますと。このとき、「λ」 は「正規化係数」と呼ばれるものであると。
\begin{eqnarray} w = (\lambda \mathbf{\mathit{I}} + \phi^T \phi )^{-1} \phi^T{t} \end{eqnarray}
というわけで、「頻度主義」の「線形回帰」と「ベイズ主義」の「ベイズ線形回帰」はどちらも同様の結論を得られるようです。
HatenaブログとMathJax.js のバッティングでまたハマった...
iqujack-lequina.hatenablog.com
⇧ 上記サイト様の方法で回避できました。
Hatenaブログって、本当に他のJavaScriptとの相性悪いな~。
今回も、モヤモヤでいっぱいですが、少しずつ勉強していきたいですね。
今回はこのへんで。

