前述の通り、ハリケーンは、女性名と男性名を交互に使用することによって命名されているが、イリノイ大学が発表した調査結果によれば、女性名が付けられたハリケーンの方が、男性名が付けられたハリケーンよりも死者数が多く、被害が大きくなる傾向にあるという。
この理由は、女性名の方が男性名よりも穏やかな印象を与える傾向にあることにあり、女性名ハリケーンの場合、男性名ハリケーンよりも、危険度が低いと人々が思い込んでしまい、その結果避難せずに被災する人が多くなるのだという。
⇧ 衝撃なんですけど...
命名法を変えた方が良いんじゃ...
ハリケーンに巻き込まれたら抜け出すのは困難ですが、今回は「機械学習(ML:Machine Learning)」とかに関係してくる「勾配法」とかについて調べてみました。
レッツトライ~。
機械学習(ML:Machine Learning)と深層学習(Deep Learning)の関係って?
まずは、Wikipediaさんに聞いてみた。
■機械学習(ML:Machine Learning)
機械学習(きかいがくしゅう、英: Machine Learning)とは、経験からの学習により自動で改善するコンピューターアルゴリズムもしくはその研究領域で、人工知能の一種であるとみなされている。「訓練データ」もしくは「学習データ」と呼ばれるデータを使って学習し、学習結果を使って何らかのタスクをこなす。例えば過去のスパムメールを訓練データとして用いて学習し、スパムフィルタリングというタスクをこなす、といった事が可能となる。
機械学習という名前は1959年にアーサー・サミュエルによって造語された。
機械学習のタスクは、以下の代表的な3種類のカテゴリーに分けられる。ただしこれらの3つで機械学習で扱う全てのタスクをカバーしているわけではないし、複数のカテゴリーに属するタスクや、どのカテゴリーに属するのか曖昧なタスクもある。
⇧ ザックリと
でカテゴリーに分けられるらしい。
■深層学習(Deep Learning)
ディープラーニング(英: Deep learning)または深層学習(しんそうがくしゅう)とは、対象の全体像から細部までの各々の粒度の概念を階層構造として関連させて学習する手法のことである。
ジェフリー・ヒントンの研究チームが実現した多層ニューラルネットワークによる手法が有名で、その派生が深層学習の中では最も普及した手法になっているが、学界では更に抽象化された数学的概念によるディープラーニングが研究されている。
深層学習として最も普及した手法は、(狭義には4層以上の)多層の人工ニューラルネットワーク(ディープニューラルネットワーク、英: deep neural network; DNN)による機械学習手法である。
要素技術としてはバックプロパゲーションなど、20世紀のうちに開発されていたものの、4層以上の深層ニューラルネットについて、局所最適解や勾配消失などの技術的な問題によって十分学習させられず、性能も芳しくなかった。
⇧ ってな感じで、最近だと「多層ニューラルネットワーク」以外も研究されてるみたいらしんですが、「多層ニューラルネットワーク」が有名ですと。
「ニューラルネットワーク」はと言うと、
ニューラルネットワーク(神経網、英: neural network、略称: NN)は、脳機能に見られるいくつかの特性に類似した数理的モデルである。「マカロックとピッツの形式ニューロン」など研究の源流としては地球生物の神経系の探求であるが、その当初から、それが実際に生物の神経系のシミュレーションであるか否かについては議論があるため人工ニューラルネットワーク (artificial neural network、ANN) などと呼ばれることもある。生物学と相互の進展により、相違点なども研究されている。
ニューラルネットワークは、教師信号(正解)の入力によって問題に最適化されていく教師あり学習と、教師信号を必要としない教師なし学習に分けられることがあるが、本質的には教師なし学習と教師あり学習は等価である。三層以上のニューラルネットワークは可微分で連続な任意関数を近似できることが証明されている。
⇧ ってな感じで、「機械学習(ML:Machine Learning)」も関係してますと。
そんな
- 「機械学習(ML:Machine Learning)」
- 「深層学習(DL:Deep Learning)」
- 「ニューラルネットワーク(NN:Neural Network)」
の関係は?
⇧ みたいな感じらしいです。
学界で研究されてるらしい「抽象化された数学的概念によるディープラーニング」ってのが出てくるとすれば変わってくるかもしれませんが、今んところは「機械学習(ML:Machine Learning)」「ニューラルネットワーク(NN:Neural Network)」の手法の中の「多層ニューラルネットワーク」ってのを利用してるのが「深層学習(DL:Deep Learning)」ってことみたいね。
で、「深層学習(DL:Deep Learning)」のアルゴリズムについては、
⇧ 有識者により様々な高性能なものが出ててますと。
「ニューラルネットワーク(NN:Neural Network)」に焦点を当てると、「深層学習(DL:Deep Learning)」は、
⇧『「隠れ層」が複数となっているものが「深層学習(DL:Deep Learning)」』ということになるらしいので、
⇧ 上図のように「隠れ層」が1つの場合は、「機械学習(ML:Machine Learning)」に該当するってことですかね?
ニューラルネットワーク(NN:Neural Network)のコンセプトと活性化関数
「ニューラルネットワーク(NN:Neural Network)」 のコンセプトとはと言うと、
ニューラルネットワークはシナプスの結合によりネットワークを形成した人工ニューロン(ノード)が、学習によってシナプスの結合強度を変化させ、問題解決能力を持つようなモデル全般を指す。
⇧ ってな感じで、人間の脳の情報伝達に着想を得ていますと。
ちなみに、
脳の10パーセント神話(のうの10パーセントしんわ、英: ten percent of the brain myth)とは、「ほとんど、あるいはすべての人間は脳の10%かそれ以下の割合しか使っていない」という長く語り継がれている都市伝説である。この伝説の誤った引用元として、アルベルト・アインシュタインを含む多数の異なる人物が示されることがある。
神経学者のバリー・ゴードンはこの伝説は嘘であると語った上で「事実上、我々は脳のすべての領域を使っているし、脳のほとんどの部分はいつでも活発だ」とつけ加えた。神経科学者のバリー・ベイヤーズテインは10%伝説の誤りを証明する7種類の証拠を提示した。
⇧ ってな感じで、「脳」については謎が多過ぎるのですが、「ニューラルネットワーク(NN:Neural Network)」ってのは、
機械学習における人工ニューラルネットワーク(ANN:Artificial Neural Network)は、人間における生体ニューラルネットワーク(BNN:Biological Neural Network)の基本的な挙動を模倣している。そのBNNでは、生体ニューロンが活性化(activation)することによって、電気信号がそのニューロンから次のニューロンへと伝播(でんぱ、※「伝搬:でんぱん」ではないので注意)していくことになる。ANNで、この「活性化」を表現するのが、活性化関数である。
⇧ こんな感じの仕組みになってますと。
確かに、我々人間においても、思い出せることがあったりなかったりするわけで、思い出せることについては、情報が次々に伝達していくであろうと。
この「どれだけの情報量が与えられれば次のニューロンに情報が伝播されていくか」ってのを決めてるのが「活性化関数」ってものですと。
なので、「隠れ層」の要素の1つ1つが、「入力値をすべて合計」「合計された入力値を活性化関数が判定」って処理をして、次の「隠れ層」ないし「出力層」へ情報を連携していきますと。
「機械学習(ML:Machine Learning)」というと、大きく分けて、
- 回帰問題(Regression Problem)
- 分類問題(Classification Problem)
があると思われますが、
⇧ というように「活性化関数」も様々ですと。
Wikipediaさんの説明によると、
活性化関数(かっせいかかんすう、英: activation function)もしくは伝達関数(でんたつかんすう、英: transfer function)とは、ニューラルネットワークのニューロンにおける、入力のなんらかの合計(しばしば、線形な重み付け総和)から、出力を決定するための関数で、非線形な関数とすることが多い。
⇧ という感じですと。
多層の「ニューラルネットワーク(NN:Neural Network)」が「深層学習(Deep Learning)」ってわけだから、「ニューラルネットワーク(NN:Neural Network)」についての考えは、そのまま「深層学習(Deep Learning)」にも当てはめることができるということかと。
ニューラルネットワーク(NN:Neural Network)で学習はどうしてる?
まぁ、情報の伝達が行われていく仕組みは何となくイメージできたわけなんだけども、肝心の「学習」はどうなってるのか?
結論から言うと、モデルの精度を高めるためには、予測した値と実際の正しい値との誤差を最も小さくすればいいです。
知識ゼロで機械学習・AIを理解するために必要なニューラルネットワークの基礎知識 | 技術ブログ | MIYABI Lab
まずは、予測値と正解ラベルとの誤差を評価するために損失関数を用います(下の図の中央部)。
知識ゼロで機械学習・AIを理解するために必要なニューラルネットワークの基礎知識 | 技術ブログ | MIYABI Lab
⇧ という感じで、「出力層」がたたき出した値は「予測値」になると思うんだけど、「予測値」と「実際の値(モデルを検証するためのテストデータなど)」の間の「誤差」の値を最小にできれば(データが1000000件あれば、1000000個の誤差がある)、「学習」できてるかどうかが分かるわけで、そのための関数を「損失関数(目的関数とも)」というそうな。
目的関数 ⊃ コスト関数、誤差関数、損失関数
目的関数が最も大きな枠組みです。
つまり、コスト関数も誤差関数も損失関数も、目的関数です。
但し書
ただ、意見が分かれているので、各参考文献や教科書など、数式を見て判断るのがよさそうです。
まあ、私レベルであれば全部なんとなく一緒とおもっていても大丈夫そうです!
⇧ という感じで、「コスト関数」「誤差関数」「損失関数」「目的関数」については認識合わせしといたほうが良さ気ですかね。
で、「誤差」を「最小」にする値を見つけるためのアプローチとして「損失関数(目的関数とも)」を微分した時の「傾き」を「最小」にする点を見つければ良いんじゃないの?ってことで「勾配法」が出てきますと。
勾配法って?
Wikipediaさんによりますと、
⇧ ってな説明で、
「最適化問題」はというと、
最適化問題(さいてきかもんだい、英: optimization problem)とは、特定の集合上で定義された実数値関数または整数値関数についてその値が最小(もしくは最大)となる状態を解析する問題である。こうした問題は総称して数理計画問題(すうりけいかくもんだい、英: mathematical programming problem, mathematical program)、数理計画とも呼ばれる。
最適化問題は目的関数や制約条件の種類によっていくつかの問題クラスに分けることができる。
⇧ ってな感じで、「最適化問題」は様々あるわけですが、
⇧ という感じみたいです。
超ザックリ言うと、「微分」して「傾き」を算出する感じですかね。
最急降下法(GD:Gradident Descent)って何?
Wikipediaさんによりますと、
Gradient descent is a first-order iterative optimization algorithm for finding a local minimum of a differentiable function. The idea is to take repeated steps in the opposite direction of the gradient (or approximate gradient) of the function at the current point, because this is the direction of steepest descent. Conversely, stepping in the direction of the gradient will lead to a local maximum of that function; the procedure is then known as gradient ascent.
Gradient descent is generally attributed to Cauchy, who first suggested it in 1847, but its convergence properties for non-linear optimization problems were first studied by Haskell Curry in 1944.
最急降下法(さいきゅうこうかほう、英: Gradient descent, steepest descent)は、関数(ポテンシャル面)の傾き(一階微分)のみから、関数の最小値を探索する連続最適化問題の勾配法のアルゴリズムの一つ。勾配法としては最も単純であり、直接・間接にこのアルゴリズムを使用している場合は多い。最急降下法をオンライン学習に改良した物を確率的勾配降下法と呼ぶ。
⇧ まぁ、何て言うか紛らわしい命名となってるようですが、「勾配降下法」と言われることもあるみたいですね。
確率的勾配降下法(SGD:Stochastic Gradient Descent)って何?
Wikipediaさんによると、
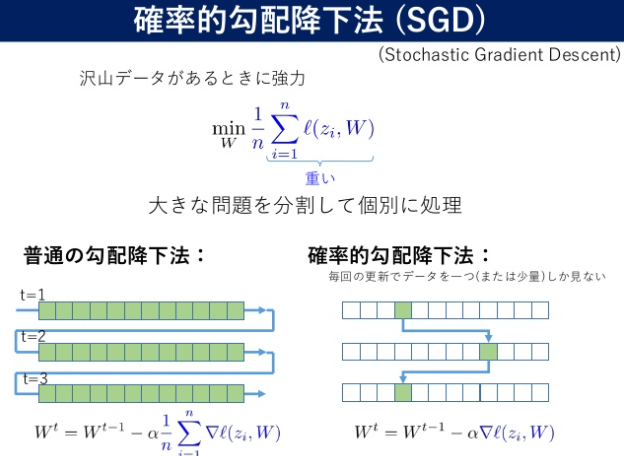
確率的勾配降下法(かくりつてきこうばいこうかほう、英: stochastic gradient descent, SGD)とは、連続最適化問題に対する勾配法の乱択アルゴリズム。目的関数が、微分可能な和の形である事が必要。バッチ学習である最急降下法をオンライン学習に改良した物。
確率的勾配降下法の収束性は凸最適化と確率近似の理論を使い解析されている。目的関数が凸関数もしくは疑似凸関数であり、学習率が適切な速度で減衰し、さらに、比較的緩い制約条件を付ければ、確率的勾配降下法はほとんど確実に最小解に収束する。目的関数が凸関数でない場合でも、ほとんど確実に局所解に収束する。これは Robbins-Siegmund の定理による。
⇧ まぁ、「最急降下法(勾配降下法)」の改良版ってことですと。
⇧ 通常の「最急降下法(勾配降下法)」が毎回すべてのデータを足し合わせて「目的関数」を算出する必要があるのに対し、「確率的勾配降下法(SGD:Stochastic Gradient Descent)」は、すべてのデータからランダムに抽出して「目的関数」を算出するので、省メモリってことみたいね。
データが(千万無量数)件とかあっても「確率的勾配降下法(SGD:Stochastic Gradient Descent)」なら省メモリだから安心!ってことですかね。
最急降下法(勾配降下法)の問題点とは
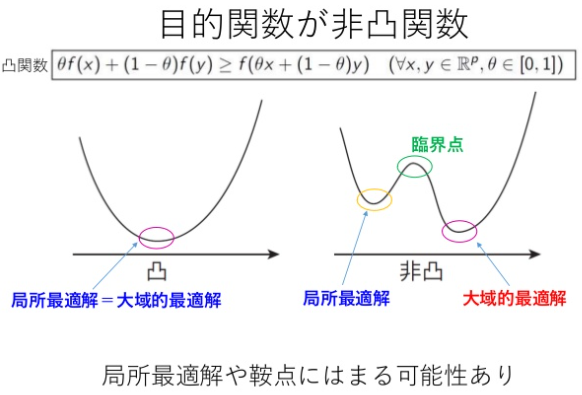
どうやら「非凸関数」を扱う上で起こり得る問題らしいです。
⇧ 上記サイト様が詳しいですが、「非凸関数」だと「目的関数」が上図のような谷がいくつもあるような関数の形になり得ますと。
そうなってくると、「最急降下法(勾配降下法)」だと、「大局的最適解」になる前に「局所最適解」を見つけてしまうと、「局所最適解」に決定されてしまうという問題があるようです。
「鞍点」はというと、
鞍点(あんてん、saddle point)は、多変数実関数の変域の中で、ある方向で見れば極大値だが別の方向で見れば極小値となる点である。
⇧ って説明なんですが、「局所解」と「鞍点」の違いがいまいちよく分からん...
多変数多峰目的関数と凸集合の(制約)条件$S$をもつ連続最適(最小)化問題における停留点として,局所解(局小値集合)とは別に鞍点の定義があるが,一般的な鞍点の定義は殆ど知られていない。本報告では方向と近傍を用いた鞍点に関わる3種の定義(鞍点,狭義鞍点,孤立鞍点)とレベル集合を用いた鞍値集合を示し,鞍値集合が孤立鞍値集合を含むことを示す。
⇧ 上記サイト様によりますと、「局所解」と「鞍点」は別物でありそうな感じはしそうですが...
ネット検索してたら、
以下の図のように、勾配が0になる点は複数あるので、この辺が最適化問題の難しい所になりそうですね(ある側面から見ると最小値でも、別の側面から見ると最大値をとる鞍点という点もあるようです)。

⇧ 上記サイト様の説明が分かりやすいです。「鞍点」ってのは、不安定な状態にあるということですね。
話が脱線しましたが、「損失関数(目的関数とも)」の目的っていうのは、「誤差」を「最小」にするっていうことだったので、「局所最適解」ではなく「大域的最適解」である必要があるわけですと。
確率的勾配降下法(SGD:Stochastic Gradient Descent)が局所解を抜け出せる可能性があるらしい
「最急降下法(勾配降下法)」だと「局所最適解」を覆すことはできないわけですが、「確率的勾配降下法(SGD:Stochastic Gradient Descent)」 であれば、「局所最適解」から抜け出せる可能性があるらしいのですと。
ここでいうThe total gradientとはバッチ学習での最急降下法です。『最急降下法では、局所解から逃げることはできないが、確率的勾配降下法(stochastic gradient)は乱数の挙動のおかげで局所解から脱出することができる』と書かれています。確かに、「確率的勾配降下法が局所解に陥らないことを断言はできないが、それでも脱出できる可能性はある」ぐらいの言い回しなら納得できます。
⇧ という感じで、あくまで「可能性」があるレベルではありますが、「最急降下法(勾配降下法)」では「局所最適解」から抜け出すことはできないことを考えれば大きな一歩ということなんですかね。
「確率的」って言葉からも、「局所最適解」から抜け出せるかどうかは神のみぞ知る世界ということでしょうか...
これは、おそらく、「局所最適解」から抜け出すための「最適解」は見つけられないから、こんな不毛なところで知的リソースを消費するのを避けるために「確率的勾配降下法(SGD:Stochastic Gradient Descent)」を採用することを一旦「最適解」とすることで、もっと他の重要な問題を考えましょうよ、っていう合意があったというような感じでしょうかね。
ちなみに、「確率的勾配降下法(SGD:Stochastic Gradient Descent)」を改良したアルゴリズムがバシバシ出ているようですが、おそらくどのアルゴリズムについても『「局所最適解」を抜け出せる可能性がある』というところに落ち着いているんではないでしょうか。
とは言え、何故に「確率的勾配降下法(SGD:Stochastic Gradient Descent)」は「局所最適解」から抜け出せる可能性があるのか?
最小値へのたどり着き方

最急降下法がほぼ直線的に最小値にたどり着くのに対し、確率的勾配降下法はランダムなのでくねくねしながら最小値にたどり着きます。
ディープラーニング(深層学習)を理解してみる(勾配降下法:最急降下法と確率的勾配降下法) - デジタル・デザイン・ラボラトリーな日々
局所解に陥る可能性
誤差関数が素直なカーブのみならいいですが、下図のようにいったん下がってまた上がるみたいなうねうねした場合があります。本当は④が最小値なのに別の小さな谷(これを局所解といいます)に捕まってしまうことがあります。

確率的勾配降下法はこのうねうねのいろいろなところから勾配を下ろうとするため、最急降下法よりも局所解に陥る可能性が小さくなります。
ディープラーニング(深層学習)を理解してみる(勾配降下法:最急降下法と確率的勾配降下法) - デジタル・デザイン・ラボラトリーな日々
⇧ 上記サイト様の図がイメージしやすいかと。
「最急降下法(勾配降下法)」だと進路が決められないのに対し、「確率的勾配降下法(SGD:Stochastic Gradient Descent)」は神出鬼没じゃないけれどもあっちいったりこっちいったりで進路を変えられるってことから『「局所最適解」を抜け出せる可能性がある』ってことみたいです。
確率的勾配降下法(オンライン学習)では、Q(w) の勾配は、1つの訓練データから計算した勾配で近似する。
上記の更新を1つ1つの訓練データで行い、訓練データ集合を一周する。収束するまで訓練データ集合を何周もする。一周するたびに訓練データはランダムにシャッフルする。AdaGrad などの適応学習率のアルゴリズムを使用すると収束が速くなる。
⇧ という感じで、ランダムにデータを使ってるという点で、「局所最適解」を回避できる場合があるってことなのかね。
宝くじと同じ理屈ってことかね...
いまは、「確率的勾配降下法(SGD:Stochastic Gradient Descent)」を改良したアルゴリズムがいろいろ出てるみたいですね、「確率的勾配降下法(SGD:Stochastic Gradient Descent)」のWikipediaにいろいろ紹介されてます。
ちなみに、「複素NN(NN:Neural Network)」って世界になってくると、
複素 MLP を学習する方法として探索空間の勾配を用いる複素パックプロパゲーション法(C-BP)や,勾配と Hesse 行列の逆行列の近似を用いる準 Newton法の一種の複素 BFGS 法(C-BFGS)などがある。
https://www.sice.or.jp/wp-content/uploads/file/ci/8thCI-1.pdf
C-BFGS は C-BP よりも効率良く探索空間を降下できるが,複素 MLP の探索空間には,実 MLP と同様,勾配がゼロの特異領域や局所最適解が多数存在する問題がある。
そのため,C-BFGS を用いたとしても常に良質の解が得られるとは限らない。
https://www.sice.or.jp/wp-content/uploads/file/ci/8thCI-1.pdf
隠れユニット数が J 個の複素 MLP(複素 MLP(J))の探索空間上の特異領域は複素 MLP(J − 1) の最適解に可約性写像を適用すると形成される。このように形成された特異領域上の複素 MLP(J) の出力は,可約性写像を適用した複素 MLP(J − 1) の最適解の出力と等
しく,また,このような特異領域上のほとんどの点は降下するルートが存在する鞍点である。
https://www.sice.or.jp/wp-content/uploads/file/ci/8thCI-1.pdf
この性質を利用し,特異領域を回避するのではなく,逆に利用する探索法である複素特異階段追跡法(C-SSF: Complex Singularity Stairs Following)1.3 が提案された。
この方法は複素 MLP(J − 1) の最適解と出力が等しい特異領域から探索空間を降下するため,隠れユニットの増加に伴って訓練誤差が単調減少する。また,現在の探索が以前の探索経路と合流する場合は現在の探索を枝刈りする手法と,特異領域上の Hesse 行列の固有値を基に探索の優先順位を決定し,探索数の上限を設定する手法により高速化された。
https://www.sice.or.jp/wp-content/uploads/file/ci/8thCI-1.pdf
研究代表者
中野 良平(NAKANO, Ryohei)
中部大学・工学部・教授
研究成果の概要(和文):実多層パーセプトロンの学習法として、探索空間の特異領域を利用して一連の隠れユニット数の最適解を系統的に求める特異階段追跡法SSFを開発し、解品質の良さと高速性を実験で確認した。また、複素多層パーセプトロンの学習法として、Wirtinger微分を用いつつ、特異領域を利用して一連の隠れユニット数の最適解を系
統的に求める複素特異階段追跡法C-SSFを開発し、優秀な適合性能を対数 旋近似やカオス予測問題で確認した。
https://kaken.nii.ac.jp/file/KAKENHI-PROJECT-25330294/25330294seika.pdf
⇧「複素特異階段追跡法(C-SSF :Complex Singularity Stairs Following)」ってものの研究が進んでるそうな。
「特異領域」ってのが何なのかはよく分からんけど、「特異領域」に存在する点は「鞍点」であることが多いんだそうな。
「MLP(Multi-Layer Perceptron)」ってのは、
多層パーセプトロン(たそうパーセプトロン、英: Multilayer perceptron、略称: MLP)は、順伝播型ニューラルネットワークの一分類である。MLPは少なくとも3つのノードの層からなる。入力ノードを除けば、個々のノードは非線形活性化関数を使用するニューロンである。MLPは学習のために誤差逆伝播法(バックプロパゲーション)と呼ばれる教師あり学習手法を利用する。その多層構造と非線形活性化関数が、MLPと線形パーセプトロンを区別している。MLPは線形分離可能ではないデータを識別できる。
多層パーセプトロンは時折、特に単一の隠れ層を持つ時、「バニラ」ニューラルネットワークと口語的に呼ばれることがある。
⇧ ってことみたいね。
より広い意味の言葉として「ニューラルネットワーク」がありますが、多層パーセプトロンはその中でも
・情報の伝達が一方向にのみ行われる
・ユニットが層状に配置される
・再帰的な接続を持たない
といった特徴を持ちます。
まぁ、毎度モヤモヤ感が半端ないんだけど...
今回はこのへんで。