Javaでオイラーの公式を表現してみたかったけど...

オイラーの公式は、変数 $θ$ が実数である場合には、右辺は実空間上で定義される通常の三角関数で表され、虚数の指数関数の実部と虚部がそれぞれ角度 $θ$ に対応する余弦関数 $cos$ と正弦関数 $sin$ に等しいことを表す。このとき、偏角 $θ$ をパラメータとする曲線 $e iθ$ は、複素平面上の単位円をなす。特に、 $θ = π$ のとき（すなわち偏角が 180 度のとき）、

e^{i\pi }=-1

となる。この関係はオイラーの等式 (Euler's identity) と呼ばれる。

オイラーの公式 - Wikipedia

$θ$ が純虚数である場合には、左辺は実空間上で定義される通常の指数関数であり、右辺は純虚数に対する三角関数となる。

オイラーの公式は、三角関数 $cos θ, sin θ$ が双曲線関数 $cosh (iθ), sinh (iθ)/ i$ に対応することを導く。また応用上は、オイラーの公式を経由して三角関数を複素指数関数に置き換えることで、微分方程式やフーリエ級数などの扱いを簡単にすることなどに利用される。

オイラーの公式 - Wikipedia

⇧ サッパリですな... そう！、サッパリ分からんのだよっ！

www.gachitan.com

⇧ 上記サイト様が、解説してくれています。

Wikipediaさんが言うように、「 $θ$ が実数である場合」であれば、

f:id:ts0818:20190831160316p:plain

http://www.ie.u-ryukyu.ac.jp/~k078521/works/math/euler.html

⇧ 上記サイト様の図にあるように、螺旋の軌道になるであろうと。

おそらく、こういう平面を、

f:id:ts0818:20190831163958p:plain

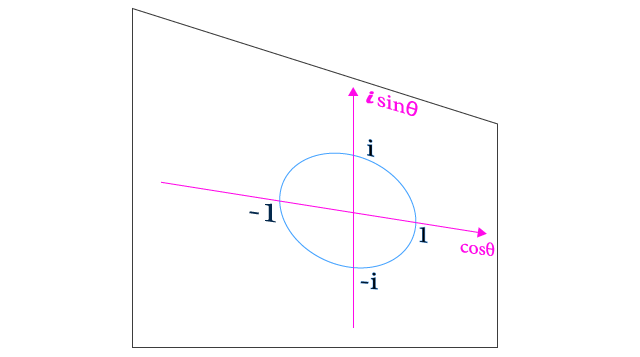
並べているんでしょうね。

f:id:ts0818:20190831163736p:plain

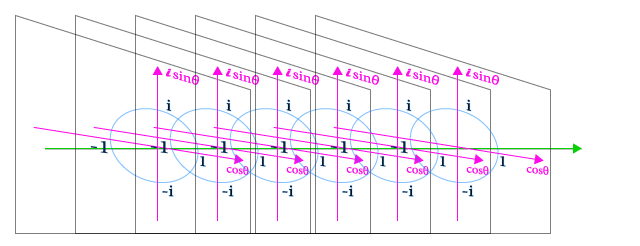
⇧ 緑の矢印が、微分・積分でいうところの、t みたいなものですかね。

それぞれの座標を繋げていくと、螺旋になるってことであろうと。本来なら数えきれないぐらい並べているのではないかと。じゃないと、きれいな螺旋にならんと思うし。

まぁ、なんとなくなザックリしたイメージだけは分かったということで。

Java でオイラーの公式を実装してみる

ということで、いざ、実装。

$e^{{i\theta }}=\cos \theta +i\sin \theta .$

をプログラミングで表すわけなんですが、虚数 i をどう実装すれば良いのか...

複素数で表現するらしい。

数学における複素数（ふくそすう、英: complex number）は、実数の対 $a, b$ と $1$ と線型独立な（実数ではない）要素 $i$ の線型結合 $a + bi$ の形に表される数（二元数: 実数体上の二次拡大環の元）で、基底元 $i$ はその平方が $-1$ になるという特別な性質を持ち虚数単位と呼ばれる。

複素数 - Wikipedia

つまり、虚数、単独での表現というのは難しいというのか、できない？らしい。つまり、i を求めようとすると、 $a + bi$ というセットで考えないと駄目ってことなんですかね？

で、残念ながら、Java の標準の API では、複素数を扱うものがいまのところ無いらしい。（将来的に、Javaの標準APIとして導入されないのかな？）

wasan.hatenablog.com

⇧ 上記サイト様によりますと、Apache Commons のライブラリには、複素数を扱うAPI が存在するらしい。

Apache Commons Math（アパッチ・コモンズ・マス）は、ApacheのトッププロジェクトであるApache CommonsにあるApache Commons#Commons Properに属する自己完結した数学と統計学の軽量コンポーネントである。統計解析、複素数演算、分数演算、行列演算、固有値問題、QR法、数値積分、多変量解析、差分法などのライブラリを持つ。

Apache Commons Math - Wikipedia

⇧ おそらく、これの、複素数演算ってライブラリで実現できるってことかしら？

オライリーも複素数っぽいものを公開してくれてたっぽいですが、作成されたのが、1997年...時代を感じさせてくれます。

resources.oreilly.com

ちなみに、オライリーのソースコードはこんな感じ。

// This example is from _Java Examples in a Nutshell_. (http://www.oreilly.com)
// Copyright (c) 1997 by David Flanagan
// This example is provided WITHOUT ANY WARRANTY either expressed or implied.
// You may study, use, modify, and distribute it for non-commercial purposes.
// For any commercial use, see http://www.davidflanagan.com/javaexamples

/**
 * This class represents complex numbers, and defines methods for performing
 * arithmetic on complex numbers.
 **/
public class ComplexNumber {
  // These are the instance variables.  Each ComplexNumber object holds
  // two double values, known as x and y.  They are private, so they are
  // not accessible from outside this class.  Instead, they are available 
  // through the real() and imaginary() methods below.
  private double x, y;

  /** This is the constructor.  It initializes the x and y variables */
  public ComplexNumber(double real, double imaginary) {
    this.x = real;
    this.y = imaginary;
  }

  /** 
   * An accessor method.  Returns the real part of the complex number.
   * Note that there is no setReal() method to set the real part.  This means
   * that the ComplexNumber class is "immutable".
   **/
  public double real() { return x; }

  /** An accessor method.  Returns the imaginary part of the complex number */
  public double imaginary() { return y; }

  /** Compute the magnitude of a complex number */
  public double magnitude() { return Math.sqrt(x*x + y*y); }

  /** 
   * This method converts a ComplexNumber to a string.  This is a method of
   * Object that we override so that complex numbers can be meaningfully
   * converted to strings, and so they can conveniently be printed out with
   * System.out.println() and related methods
   **/
  public String toString() { return "{" + x + "," + y + "}"; }

  /** 
   * This is a static class method.  It takes two complex numbers, adds them, 
   * and returns the result as a third number.  Because it is static, there is
   * no "current instance" or "this" object.  Use it like this:
   * ComplexNumber c = ComplexNumber.add(a, b);
   **/
  public static ComplexNumber add(ComplexNumber a, ComplexNumber b) {
    return new ComplexNumber(a.x + b.x, a.y + b.y);
  }

  /**
   * This is a non-static instance method by the same name.  It adds the
   * specified complex number to the current complex number.  Use it like this:
   * ComplexNumber c = a.add(b);
   **/
  public ComplexNumber add(ComplexNumber a) {
    return new ComplexNumber(this.x + a.x, this.y+a.y);
  }

  /** A static class method to multiply complex numbers */
  public static ComplexNumber multiply(ComplexNumber a, ComplexNumber b) {
    return new ComplexNumber(a.x*b.x - a.y*b.y, a.x*b.y + a.y*b.x);
  }

  /** An instance method to multiply complex numbers */
  public ComplexNumber multiply(ComplexNumber a) {
    return new ComplexNumber(x*a.x - y*a.y, x*a.y + y*a.x);
  }
}

というわけで...って、まったく、虚数 i についての記述が見られんのだが...駄目じゃないの、これ...

写経チックに記述してみましたが...

f:id:ts0818:20190831231958p:plain

/TestEuler/src/main/TestComplexNumber.java

package util;

public class ComplexNumber {
  private double real, imaginary;

  public ComplexNumber() {

  }

  public ComplexNumber(double real, double imaginary) {
    this.real = real;
    this.imaginary = imaginary;
  }

  public double getReal() {
    return (real);
  }

  public void setReal(double real) {
    this.real = real;
  }

  public double getImaginary() {
    return (imaginary);
  }

  public void setImaginary(double imaginary) {
    this.imaginary = imaginary;
  }

  public ComplexNumber multiply(ComplexNumber factor) {
    ComplexNumber product = new ComplexNumber();

    product.setReal((real * factor.real) - (imaginary * factor.imaginary));
    product.setImaginary((imaginary * factor.real) + (real * factor.imaginary));
    return (product);
  }

  public ComplexNumber divide(ComplexNumber divisor) {
    ComplexNumber quotient = new ComplexNumber();

    quotient.setReal(((real * divisor.real) + (imaginary * divisor.imaginary))
        / (double) (Math.pow(divisor.real, 2) + Math.pow(divisor.imaginary, 2)));
    quotient.setImaginary(((imaginary * divisor.real) - (real * divisor.imaginary))
        / (double) (Math.pow(divisor.real, 2) + Math.pow(divisor.imaginary, 2)));
    return (quotient);
  }
}

/TestEuler/src/util/ComplexNumber.java

package main;

import util.ComplexNumber;

public class TestComplexNumber {

  public static void main(String[] args) {
    // 
    double theta = Math.PI / (double)2;
    System.out.println("cos： " + Math.cos(theta));
    System.out.println("sin： " + Math.sin(theta));
    ComplexNumber ei = new ComplexNumber(Math.cos(theta), Math.sin(theta));
    System.out.println(ei.getReal() + " + " +  ei.getImaginary());
    
  }
}

んで実行してみる。

f:id:ts0818:20190831232434p:plain