標準偏差（standard deviation）って何ぞ？

f:id:ts0818:20190503204607j:plain

judge.u-aizu.ac.jp

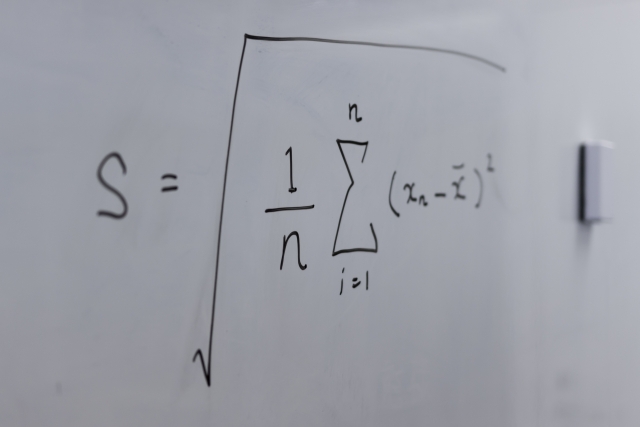
⇧ 上記サイト様を利用させていただいてますが、ついに未知の概念「標準偏差」なるものが出てきてしまったので調査していこうかと。

標準偏差（standard deviation）って何？

例によって、Wikipediaさんに聞いてみた。

標準偏差（ひょうじゅんへんさ、英: standard deviation, SD）は、日本工業規格では、分散の正の平方根と定義している。データや確率変数の散らばり具合（ばらつき）を表す数値の一つ。物理学、経済学、社会学などでも使う。例えば、ある試験でクラス全員が同じ点数、すなわち全員が平均値の場合、データにはばらつきがないので、標準偏差は $0$ になる。

標準偏差 - Wikipedia

⇧ う～ん、分からん...

母集団や確率変数の標準偏差を $σ$ で、標本の標準偏差を $s$ で表すことがある。二乗平均平方根 (RMS) と混同されることもある。両者の差異については、二乗平均平方根を参照。

標準偏差 - Wikipedia

⇧ 「二乗平均平方根」ってのとは別物であると。

二乗平均平方根（にじょうへいきんへいほうこん、英 : root mean square, RMS）はある統計値や確率変数を二乗した値の平均値の平方根である。結果として単位が元の統計値・確率変数と同じという点が特徴である。また、計算が積和演算であるため高速化が容易である。絶対値の平均より、用いられることがある。

二乗平均平方根 - Wikipedia

「標準偏差」と「二乗平均平方根」は、求めるときの式の形が異なると。「標準偏差」については、

母集団の標準偏差
標本の標準偏差

の2つが存在するらしい。

母集団の標準偏差

$n$ 個のデータ $x 1, x 2, \dots, x n$ からなる母集団を考える。その母集団の平均（または母平均） $μ$ は、次の通りに定義される:

\mu ={\frac {1}{n}}\sum _{i=1}^{n}x_{i}.

このとき、母平均 $μ$ を使って次式で得られる量 $σ 2$ を分散（または母分散）と定義する。

\sigma ^{2}={\frac {1}{n}}\sum _{i=1}^{n}(x_{i}-\mu )^{2}={\frac {1}{n}}\sum _{i=1}^{n}{x_{i}}^{2}-\mu ^{2}.

この分散の非負の平方根 $σ$ を、母集団の標準偏差と定義する。分散はデータの散らばり具合を表す量であるが、元のデータを平方しているので元のデータや平均値と次元が異なり直接比較することができない。平方根をとると元のデータと同じ次元になるので、分散よりも標準偏差の方が散らばり具合を表す量として便利なことがある。

標準偏差 - Wikipedia

⇧ ( |対象1 - 対象集団の平均| $2$ + |対象2 - 対象集団の平均| $2$ + |対象3 - 対象集団の平均| $2$ + ... ... + |対象n - 対象集団の平均| $2$ ) × 1/n ってことをやって出た結果を「分散」とし、その非負の平方根を「標準偏差」というらしいと。

標本の標準偏差

母集団（nよりはるかに大きい）の中から、 $n$ 個のデータ $x 1, x 2, \dots, x n$ からなる標本を抽出したとする。このとき、標本平均を次式で定義する:

{\bar {x}}={\frac {1}{n}}\sum _{i=1}^{n}x_{i}.

この標本平均を使って次式で定義される量を標本の分散と呼ぶ。

s^{2}={\frac {1}{n}}\sum _{i=1}^{n}(x_{i}-{\bar {x}})^{2}={\frac {1}{n}}\sum _{i=1}^{n}{x_{i}}^{2}-{\bar {x}}^{2}.

標本の分散の平方根 $s$ を標本の標準偏差と呼ぶ。

$σ 2$ を母集団の分散、 $s 2$ を標本の分散とすると、

E[s^{2}]={\frac {n-1}{n}}\sigma ^{2}

となることが示される。つまり、標本の分散は母集団の分散よりも小さくなる傾向がある。そのため、標本の分散は母集団の分散の不偏推定量ではない。そこで、

u^{2}={\frac {1}{n-1}}\sum _{i=1}^{n}(x_{i}-{\bar {x}})^{2}={\frac {1}{n-1}}\sum _{i=1}^{n}{x_{i}}^{2}-{\frac {n}{n-1}}{\bar {x}}^{2}

を考えると、この量の期待値は母集団の分散に等しく、分散の不偏推定量になっている。こうして定義される $u 2$ を不偏分散という。標本分散と呼ぶこともある。

$u 2$ の平方根 $u$ を標本標準偏差ということもある。

不偏分散の平方根 $u$ は、標準偏差の不偏推定量ではない。例えば母集団が正規分布に従う場合、標準偏差の不偏推定量 $D$ は次式で与えられる。

D={\sqrt {\frac {n-1}{2}}}{\frac {\Gamma \left({\frac {n-1}{2}}\right)}{\Gamma \left({\frac {n}{2}}\right)}}u.

ここで、 $Γ$ はガンマ関数、 $u 2$ は不偏分散である。

標本サイズが大きくなれば、標準偏差の不偏推定量 $D$ は、近似的に、平均からの偏差平方和を $n - 1.5$ で割った値の平方根として求められる。

D\approx {\sqrt {{\frac {1}{n-1.5}}\sum _{i=1}^{n}(x_{i}-{\bar {x}})^{2}}}={\sqrt {{\frac {1}{n-1.5}}\sum _{i=1}^{n}{x_{i}}^{2}-{\frac {n}{n-1.5}}{\bar {x}}^{2}}}.

標準偏差 - Wikipedia

⇧ いきなり、わけの分からんことになってるけど、「分散」「標準偏差」までの算出方法は、「母集団の標準偏差」の時とほぼ変わらないっぽい。

二乗平均平方根の定義

$N$ 個の数 ${x 1, x 2,..., x N}$ について二乗平均平方根は

$\operatorname {RMS} [x]={\sqrt {{1 \over N}\sum _{i=1}^{N}x_{i}^{2}}}={\sqrt {{x_{1}^{2}+x_{2}^{2}+\cdots +x_{N}^{2}} \over N}}$

と定義される。

充分小さな $Δ x'$ に対して $x \in [x', x' + Δ x']$ となる確率を $f (x')Δ x'$ としたとき、 $x$ の二乗平均平方根 $RMS [x]$ は

$\operatorname {RMS} [x]={\sqrt {\int _{-\infty }^{+\infty }x'^{2}f(x')dx'}}$

と定義される。ここで関数 $f (x')$ は確率密度関数と呼ばれる。

連続関数 $x (t)$ の区間 $t \in [t 1, t 2] (t 1 < t 2)$ については媒介変数の積分を用いて、

$\operatorname {RMS} [x(t)]={\sqrt {{\frac {1}{t_{2}-t_{1}}}\int _{t_{1}}^{t_{2}}(x(t))^{2}\,dt}}$

と定義される。

二乗平均平方根 - Wikipedia

⇧ ( |対象1| $2$ + |対象2| $2$ + |対象3| $2$ + ... ... + |対象n| $2$ ) × 1/n ってことをやって出た結果の平方根を「二乗平均平方根」とするらしい。

まぁ、分かりにくいというか、ガッツリ数学の知識がいるやん...

「標準偏差」について、

atarimae.biz

⇧ 上記サイト様が分かりやすく説明してくれています。

標準偏差を求めるプログラム

そんでは、「標準偏差」を求める式が判明したところで、

judge.u-aizu.ac.jp

⇧ 上記の問題にトライしてみたいと思います。

Eclipseを起動し、適当なJavaプロジェクト、クラスを作成。

f:id:ts0818:20190504115435p:plain

ソースコードはこんな感じになりました。

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.List;

public class Deviation {

  public static void main(String[] args) {
    // TODO 自動生成されたメソッド・スタブ
    BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
    List<Double> sdList = new ArrayList<>(); // 標準偏差を格納するリスト

    while (true) {
      try {
        int n = Integer.parseInt(br.readLine()); // 対象の人数
        if (n == 0) { // 対象が存在しない場合
          break; // ループを抜ける
        }
        String[] score = br.readLine().split("\\s"); // 得点の配列
        double average = 0; // 平均値
        double sum = 0; // 合計値
        // 合計を算出
        for (int i = 0; i < score.length; i++) {
          sum += Double.parseDouble(score[i]);
        }
        // 平均を算出
        average = sum / (double) n;
        double a = 0; // 標準偏差
        // (Si - m)*(Si - m)の部分の値を算出
        for (int i = 0; i < n; i++) {
          a += Math.pow((Double.parseDouble(score[i]) - average), 2);
        }
        // 標準偏差を算出
        a = Math.sqrt(a / (double) n);
        // 標準偏差をリストに格納
        sdList.add(a);

      } catch (NumberFormatException e) {
        // TODO 自動生成された catch ブロック
        e.printStackTrace();
      } catch (IOException e) {
        // TODO 自動生成された catch ブロック
        e.printStackTrace();
      }
    }
    // 標準偏差を出力
    for (double sd : sdList) {
      System.out.printf("%.10f\n", sd);
    }
  }
}

んで、実行。

f:id:ts0818:20190504115347p:plain