⇧ う~む、対策が実現できるものになっていればありがたいですが...
全然関係ない話ですが、
オークランド(英: Auckland, 英語発音: [ˈɔːklənd], マオリ語: Tāmaki-makau-rau、漢字表記「奧克蘭」)は、ニュージーランド北島北部に位置するニュージーランド最大の都市。オセアニア有数の世界都市でありポリネシア地域最大の都市でもある。都会でありながら周辺に変化に富む自然環境を持っている。
オークランド(英語: City of Oakland, 英語発音: [ˈoʊklənd])は、アメリカ合衆国カリフォルニア州アラメダ郡にある、サンフランシスコ湾に面した港湾都市、アラメダ郡庁所在地。かつて日本から移民が渡った地であり、日本語で王府(おうふ)とも称した。公式的なものではないが住人をはじめ多くの人々からオークタウン (Oaktown) の愛称で呼ばれる。
⇧ 都市名が同じになってるのを知って、
⇧ 上記の記事が気になった今日この頃です。
・「帆の街City of Sails(シティ・オブ・セイルズ)」の愛称で親しまれている、ニュージーランド最大の都市オークランドは英語ではAucklandと表記されているが、Oaklandと表記するアメリカの都市と日本語での呼び方が同じなため、NZオークランドとUSオークランドと区別表記されることもある
⇧ な~るほど。
最適輸送って何?
「最適輸送の理論とアルゴリズム - Forkwell Library #18」ってイベントに参加して、「最適輸送」って言葉を知ったのだけど、「最適輸送」って何?
ネットで調べてみたところ、
⇧ 「最適化法」にカテゴライズされるものらしい。
で、参加したイベントで、『ワッサースタイン距離は距離公理を満たす最適輸送の特殊ケース』って話が出てきたので、「ワッサースタイン距離」はと言うと、
In mathematics, the Wasserstein distance or Kantorovich–Rubinstein metric is a distance function defined between probability distributions on a given metric space . It is named after Leonid Vaseršteĭn.
One way to understand the above definition is to consider the optimal transport problem.
⇧ 数学の分野で、複数の確率分布の間の距離関数ということらしく、「最適輸送問題」で考えることが理解につながるらしい、ということで「最適輸送問題」とは?
In mathematics and economics, transportation theory or transport theory is a name given to the study of optimal transportation and allocation of resources. The problem was formalized by the French mathematician Gaspard Monge in 1781.
https://en.wikipedia.org/wiki/Transportation_theory_(mathematics)
⇧ 一番コストを抑えられる輸送方法を導き出そうとすることのようです。
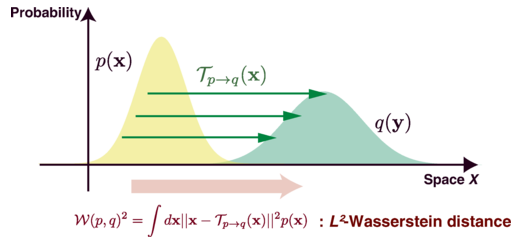
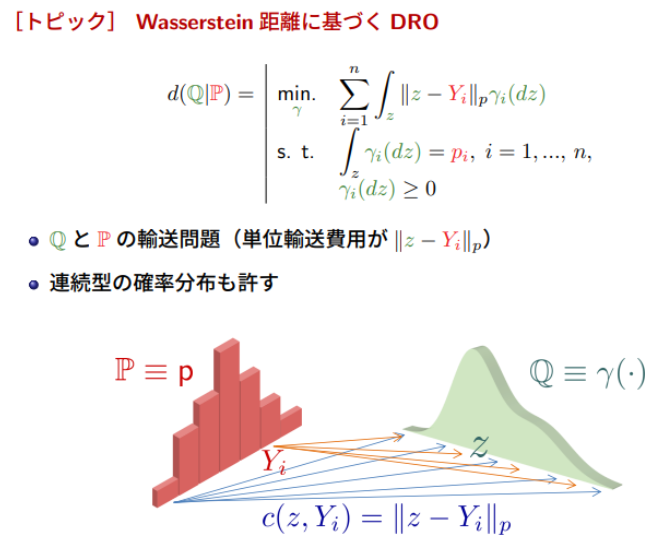
イメージ的には、
⇧ 上図のような感じらしい。
Wikipediaによると「複数の確率分布の間の距離関数」が「ワッサースタイン距離」ということなので、距離関数の値を最小化することができれば、輸送コストを抑えられることになりますと。
『ワッサースタイン距離は距離公理を満たす最適輸送の特殊ケース』ってことらしいので、「ワッサースタイン距離」以外にも様々な距離関数で「最適輸送」に合致するケースが考えられるってことなんだろうか。
ちなみに、
最適輸送理論とは ‘物質をある場所から他の場所へ最小費用で移す’ 理論です.(例えば,18世紀後半に G. Monge はどこかの土壌を削り取って運び,城を守る盛り土を作ることを考えていたようです)
https://www.kurims.kyoto-u.ac.jp/~kyodo/kokyuroku/contents/pdf/1916-11.pdf
⇧ 上記の資料によりますと、「特別な場合 (例えばユークリッド空間の場合)」って話が出てきて、「ユークリッド空間」はと言うと、
ユークリッド空間(ユークリッドくうかん、英: Euclidean space)とは、数学における概念の1つで、エウクレイデス(ユークリッド)が研究したような幾何学(ユークリッド幾何学)の場となる平面や空間、およびその高次元への一般化である。
⇧ と説明がありますと。
で、
⇧ 上記サイト様が、機械学習で出てくる距離をまとめてくださってました。
本日の成果としては、「最適輸送」に使える距離の1つが「ワッサースタイン距離」ってことなのが分かったぐらいかな...
「最適輸送」は、「勾配法」のような「最適化法」というカテゴリに属するアルゴリズムの総称って考えれば良いんかな?
毎度モヤモヤ感が半端ない...
今回はこのへんで。