
『ひょっこりひょうたん島』(ひょっこりひょうたんじま)とは、NHK総合テレビで放送された人形劇である。
⇧ 「島」というと「ひょっこりひょうたん島」を思い浮かべてしまう昭和生まれだけど時は令和、どうもボクです。
というわけで、「GDG DevFest 2020」に参加してきました~。
⇧ 上記のイベントで知ったのですが、「LeetCode」 っていうコーディングのスキルを習熟するためのサイトがあるらしく、
⇧ 上記サイトになるのですが、
⇧ いろいろ問題が用意されてるらしい。
AOJ(AIZU ONLINE JUDGE)は知ってたんだけど、「LeetCode」ってのは知らなんだ。
他にも、「AtCode」ってのが有名らしいですね。
まぁ、「アルゴリズム」は勉強できるっていう意味では、どれをとっても変わらないらしいんだけど、
外資IT企業ではソフトウェアエンジニアを雇う際にコーディング面接を非常に重視する。
業務上のコーディングよりは簡単めのプログラミングコンテスト問題に近く、アメリカの学生やエンジニアがIT企業を受ける際には事前対策を数ヶ月するのが常識になっているようだ。
ここ数年、leetcode.comというコーディング面接の過去問サイトが広く候補者に使われるようになっている。
2018年ごろにコロンビア大の学生に聞いた話では、コンピュータサイエンスの学生はほぼ全員アカウントを持っていて半数は課金しているとのこと。
面接の際は出た問題を漏らさないよう候補者に約束させることが普通だが、leetcodeは大手企業で実際に出されたと思われる問題を収集し課金ビジネスをしているので、道義的にはグレー。
⇧ 金を払えばって...裏口入学、もとい、裏口就職やないか~い!
まぁ、脱線したんですが、 「GDG DevFest 2020」で面白い問題が紹介されていたので、Javaで解いてみることに。
レッツトライ~。
Number of Islands 問題って?
日本語にすると、「島の数」ってことなんだけど、そのものズバリ、「島の数」を算出する問題らしいです。
algorithms.tutorialhorizon.com
⇧ 上記サイト様のように、
| 数値 | 内容 |
|---|---|
| 0 | 海とみなす |
| 1 | 島とみなす |
というように、「1」が固まっている部分を1つの島とカウントするという問題なのですが、これが初見だとなかなか取り組むのが難しいんですよ。
どういうアプローチをすれば良いのか?
普通、プログラミングって
| 処理 | 内容 |
|---|---|
| 順次(sequence) | サブプログラムを順々に実行する。 |
| 選択(selection) | 条件式が導出した状態に従い、次に実行するサブプログラムを選択して分岐する。 |
| 反復(repetition) | 条件式が導出した特定の状態の間、サブプログラムを繰り返し実行する。 |
⇧ 上記の3つの組み合わせで成り立っているってよく言われるんですよね。
で、「Numbers of Islands」問題ですが、先ほどのサイト様の例だと、「アタック25」みたいに要素が25ありますと。さらに、「表」として捉えることができるので、「表」と見立てた場合「行」と「列」 があるので、二重ループ(for文の入れ子)での処理は必要になりそうですと、つまり『反復』の処理は必要。
あとは、「0」か「1」を見分けにゃならんので、『選択』の処理(if文)も必要...
ってそんなことは言われんでも分かるんですが、問題は、通常の二重ループ(for文の入れ子)で処理すると、上から1行ずつ処理されるってことなんですな。
つまり、
1行目が処理されたら、2行目。2行目が処理されたら、3行目...って感じになるので、縦で繋がってる『島』を検知できない。
なので、次の行に移る前に、『島』がどういう形か把握できて、カウントできないとマズイわけですと。
じゃあ、どうすんの?
ってなると、マス目が「1」だった場合に、自分自身に隣接するマス目が「1」かどうか調べれば良い、つまり、自分自身に隣接するマス目に対しても、同じ処理をしてあげて、その処理の最中に隣接するマス目が「1」であったら、同様の処理を...って感じで処理してあげれば良いわけですと。
つまり、「再帰処理」ってものを利用すれば、イケそうですと。
実際に試してみる
Eclipseを起動して、「パースペクティブ」が「Java」になってることを確認し、

「ファイル(F)」>「新規(N)」>「Java プロジェクト」を選択で。

「プロジェクト名(P):」を適当に入力し、「完了(F)」で。

モジュールは「作成しない(D)」で。

プロジェクトが作成されたら、「src」フォルダを選択した状態で右クリックし、「新規(W)」>「クラス」を選択。

「名前(M):」を適当に入力し、「完了(F)」で。

で、コーディングしてみる。
package number_of_islands;
public class CountIslands {
public static void main(String[] args) {
// 対象
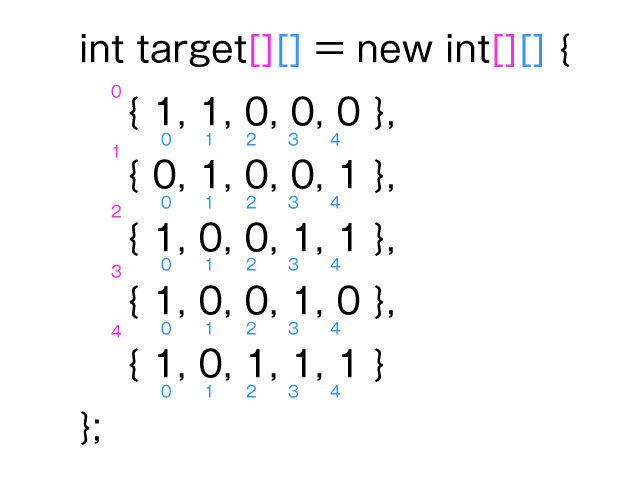
int target[][] = new int[][] {
{ 1, 1, 0, 0, 0 },
{ 0, 1, 0, 0, 1 },
{ 1, 0, 0, 1, 1 },
{ 1, 0, 0, 1, 0 },
{ 1, 0, 1, 1, 1 }
};
int result = 0; // count island
//
for (int i = 0; i < target.length; i++) {
for (int j = 0; j < target[0].length; j++) {
if (target[i][j] == 1) {
// 隣接する数字を確認
dfs(target, i ,j);
result++;
}
}
}
System.out.println(result);
}
public static void dfs(int islandGridMap[][], int row, int col) {
int limitRow = islandGridMap.length;
int limitCol = islandGridMap[0].length;
if (row < 0 || col < 0 || row >= limitRow || col >=limitCol || islandGridMap[row][col] != 1) {
return; // 処理を抜ける
}
islandGridMap[row][col] = 0; // 確認済の個所は、再度確認しないように、1以外を設定
dfs(islandGridMap, row+1, col); // 右隣り
dfs(islandGridMap, row-1, col); // 左隣り
dfs(islandGridMap, row, col+1); // 上隣り
dfs(islandGridMap, row, col-1); // 下隣り
}
}
そしたら、実施してみる。


⇧ 島の数は、「3」となったので、問題なさそうです。
Union-Find アルゴリズムで処理が改善される?
「再帰処理」はプログラミング的に、かなりリスクの高い処理であるらしいので、使わないで済むのなら極力使わないほうが良いらしいですと。
タスクに割り当てられるスタックサイズの小さな組み込み系では「再帰呼び出しはご法度」とまで言われていますし、通常の Linux や Windows 環境であっても、スタックオーバーフローについて留意することがとても重要です。
⇧ 上記サイト様によりますと、「再帰処理」は組み込み系などでは御法度とされるようですね...
で、「Union-Find」という考え方の出番ですと。
素集合データ構造(そしゅうごうデータこうぞう、英: disjoint-set data structure)は、データの集合を素集合(互いにオーバーラップしない集合)に分割して保持するデータ構造。このデータ構造に対する以下の2つの便利な操作をUnion-Findアルゴリズムと呼ぶ。
- Find: 特定の要素がどの集合に属しているかを求める。2つの要素が同じ集合に属しているかの判定にも使われる。
- Union: 2つの集合を1つに統合する。
これら2つの操作をサポートしているため、素集合データ構造は「Union-Findデータ構造」あるいは「Merge-Find集合」とも呼ばれる。これら以外の重要な操作として MakeSetがある。これは、与えられた1つの要素だけを格納した集合(シングルトン)を作成する。これら3つの操作により、様々な実用的分割問題を解くことができる(「応用」の節を参照)。
⇧ 『2つの便利な操作を「Union-Findアルゴリズム」という』、の後に、『これら以外の重要な操作として MakeSet がある。』って...
結局、3つの操作が必要やんけ~!
っていうツッコミをいれたくなるのはさて措き、「AtCoder」 のCEOが「Union-Find」についてスライドをアップロードしてくれてるみたい。
⇧ 「グループ」の中の先頭の要素を「ルート」として、その他の要素が「ルート」に紐づくように表現できるんですと。
で、「Union-Find」と、
- 経路圧縮
- ランク付け
を組み合わせることで、「計算量」を減らせるらしい。 「計算量」ってのは「処理にかかる時間」に影響しますね。
⇧ 上記がどれぐらいスゴイことなのかいまいち分からんのだけど、
以下のように普通に、グループ分けすると、
⇧ 時間がかかるんですと。
で、どれぐらい違ってくるのかと言うと、
⇧ ってな感じで、対象の数が増えると如実に影響が出てきますと。
「一瞬」と「3年ぐらい」って...格差社会が。
ちなみに「再帰処理」とかは、「地球爆発」するぐらいの時間がかかるってことね...
諸行無常...
Union-Find のアルゴリズムで実装してみる
と言うわけで、「再帰処理」を使ってると、我らが地球が「地球爆発」してしまうぐらいの悠久の時の流れを刻んでしまうこともあり得るので、「Union-Find」のアルゴリズムで実装してみようじゃないかと。
そういえば、「地球ちゃん」とかいうキャラが「半熟英雄」ってスーパファミコンのソフトで出てきたような...
はい、脱線しました。
で、「Union-Find」ですが、ソースコードを確認したところ、一旦、2次元配列を1次元配列と捉え直して考えるみたいね。
どういうことかと言うと、例えば、今回の「Numbers of Islands」の問題とかだと、以下のような、2次元配列になってると思うんだけど、
で、この2次元配列を、以下のような1次元配列と見立てた場合、

全ての要素に一意の通し番号(インデックス)が振れるわけですと。(まぁ、1次元配列とした場合、こんな表の形が維持されるわけではないのですが、2次元配列のどの要素に、1次元配列のどのインデックスがマッピングされる感じになるのかイメージし易いように、上図のような形にしてます)
で、試しに島の部分(1次元配列と見立てたイメージ図の要素の値が「1」で固まってる部分)を囲ってみると、

上図のような感じで、島(グループ)が3つできるんだけど、このとき、各グループの先頭の要素のインデックスを木(集合)のルートと見なせば、

上図みたいな木(集合)と表せるよね、ってことらしいと思うんだけど、じゃあ、実際にプログラミング上はどう処理すれば良いのよ?
ってことなんですが、上図の3つの島をそれぞれ最小単位の島に分解した場合(上図の木のそれぞれの〇を1つの島と見立てた場合)、13つの島(「0」「1」「6」「10」「15」「20」「9」「13」「14」「18」「22」「23」「24」)になるんだけど、隣接する島が見つかった場合に、「Union」されるので「-1」していくということを繰り返すと、な、何と!
今回の場合は、最終的に、島の数が3つになるんですな。
「Union」が「2つの集合を1つに統合する」という操作なので、「2つだったものを1つにするんだから、当然、1つ減る」ってことなんですな。
「0」「1」「6」の塊の島を、バラバラにした状態から考えてみると、

⇧ 上図のようになりますと。
「10」「15」「20」と「9」「13」「14」「18」「22」「23」「24」の島についても、隣接してるのが判明したら「Union」していくことで、それぞれ1つの島になるので、結果として、島の数は3つとなりますと。
「ランク付け」を導入していれば、木(集合)の長い方に短い方を「Union」できるらしいのと、
⇧ 2つの木(集合)を「Union」する場合は、木(集合)の長いほうのルートが維持されるらしいですと。
上図だと当然のように、木(集合)の長い方のルートの要素に「Union」されてるんだけど、いまいち、どの要素に「Union」されるのかの基準が分からんのだが...
というわけで、実際にプログラミングしてみると、以下のようなコーディングになりましたと。
「Union-Find」のアルゴリズム用のクラス
package number_of_islands.util;
public class UnionFindTree {
private int[] parent;
private int[] rank;
public UnionFindTree (int size) {
this.parent = new int[size];
this.rank = new int[size];
for (int i = 0; i < size; i++) {
makeSet(i);
}
}
public int[] getParent () {
return this.parent;
}
public int[] getRank () {
return this.rank;
}
// 与えられた1つの要素だけを格納した集合を作成
public void makeSet (int i) {
this.parent[i] = i;
this.rank[i] = 0; // 集合の高さ
}
// 2つの集合を1つに統合する
public void union (int x, int y) {
int rootX = find(x); // xが属する木(集合)のルート
int rootY = find(y); // yが属する木(集合)のルート
if (is_same(x, y)) { // 同じ木(集合)に属している場合は統合しない
return;
}
// ランク付け
// 木(集合)の長さを比較。長い木(集合)に短い木(集合)を統合
if (this.rank[rootX] < this.rank[rootY]) { // yが属する木(集合)のほうが長い場合
this.rank[rootX] = this.rank[rootY]; // xが属する木(集合)の長さを、yが属する木(集合)の長さに合わせる
this.parent[rootX] = rootY; // yが属する木(集合)のルートに変更
} else if (this.rank[rootX] > this.rank[rootY]) { // xが属する木(集合)のほうが長い場合
this.rank[rootY] = this.rank[rootX]; // yが属する木(集合)の長さを、xが属する木(集合)の長さに合わせる
this.parent[rootY] = rootX; // xが属する木(集合)のルートに変更
} else { // 木(集合)の長さが同じ場合
this.parent[rootY] = rootX; // どっちかに合わせる
this.rank[rootX] ++; // ルートになった方の木(集合)の長さを1つ長くする
}
}
// 特定の要素がどの木(集合)に属してるか求める
public int find (int i) {
return this.parent[i] == i ? i: find(this.parent[i]);
}
// 同じ木(集合)に属しているか
public boolean is_same (int x, int y) {
return find(x) == find(y);
}
}
実際に処理を実施するクラス。
package number_of_islands;
import number_of_islands.util.UnionFindTree;
public class CountIslands {
public static void main(String[] args) {
// 対象
int target[][] = new int[][] {
{ 1, 1, 0, 0, 0 },
{ 0, 1, 0, 0, 1 },
{ 1, 0, 0, 1, 1 },
{ 1, 0, 0, 1, 0 },
{ 1, 0, 1, 1, 1 }
};
int rowLength = target.length;
int colLength = target[0].length;
UnionFindTree unionFindTree = new UnionFindTree(rowLength * colLength);
int islandsCount = 0; // 島の数
for (int i = 0; i < target.length; i++) {
for (int j = 0; j < target[0].length; j++) {
if (target[i][j] == 1) {
islandsCount++; // 島の数をすべてカウント
// 進行方向に隣接する島があった場合の処理
if (checkRangeGrid(i+1, j, target) && target[i+1][j] ==1) { // 下に隣接する島が見つかった場合は統合
unionFindTree.union(i +1, j); // 下隣り
islandsCount--; // 統合が実施されたら、島の数は1つ減る(2つを1つにするので)
}
if (checkRangeGrid(i, j+1, target) && target[i][j+1] ==1) { // 右に隣接する島が見つかった場合は統合
unionFindTree.union(i, j +1); // 右隣り
islandsCount--; // 統合が実施されたら、島の数は1つ減る(2つを1つにするので)
}
}
}
}
System.out.println(islandsCount);
}
// 配列の要素の範囲内か確認
public static boolean checkRangeGrid (int row, int col, int[][] targetGrid) {
return (row >= 0 && col >= 0 && row < targetGrid.length && col < targetGrid[0].length);
}
}
で、こいつを実行してみると、


島の数は「3」つとなったので、「Union-Find」が機能したってことになるのかな?
島が統合されるんだから島の数はどんどん減っていくよね、って発想が意外と思いつかんかった...
確かにカウントするっていうのは「加算」だけでなく「減算」もあるんよね、そんな当たり前のことになかなか気付かんとは、頭が固くなってますな...
というか、「UnionFindTree.java」の「find」メソッドで「再帰処理」しちゃってるんだけどね...計算量が改善されないんじゃあ...、という疑問を抱えたまま今日も過ぎていく...
まぁ、いつも通り、モヤモヤ感は半端ないですが...
「Union-Find」ってアルゴリズムの存在を知れたということで良しとしますかね。
今回はこのへんで。








